Partiamo da una prima considerazione: A cosa servono le
"DISEQUAZIONI" ?
A parte il piacere che incontra la nostra mente a cimentarsi in
problemi di vario tipo (che sarebbe un po' pochino), per lo più la
"disequazione" risponde al problema di "cosa devo fare perché
qualcosa sia maggiore di qualcos'altro".
Prendiamo ad esempio questo problema (prova INVALSI 2011/2012 per le
classi II):
Nella stazione sciistica di Paperopoli a Monte (vabbé,
il nome me lo sono inventato io, nella prova invalsi era leggermente
diverso) si praticano le seguenti offerte:
- Offerta A: Abbonamento 100 € di costo iniziale + 15 € per il
giornaliero (da pagare solo per i giorni in cui si scia)
- Offerta B: Giornaliero a 30€ (senza costo iniziale, ti
presenti in biglietteria, paghi 30€ e scii tutto il giorno).
Il dilemma è sempre questo: quale delle offerte mi conviene di
più?
|
 |
|
Ovviamente se scio solo oggi non mi metto certo a spendere i 100 €
dell'abbonamento e in più i 15 del giornaliero ....
Se scio tutta la stagione è naturale che mi convenga l'abbonamento
(i 100€ iniziali dopo un po', sicuramente si "ammortizzeranno" e pagherò di
meno).
Ma devo stare qui per soli 7 giorni, e magari non scio nemmeno tutti
i giorni .. cosa mi conviene fare?
In pratica abbiamo due funzioni soldi/giorni dove se chiamiamo Y la
spesa e X i giorni di sci saranno:

Se vogliamo sapere quando la prima offerta viene a costare meno
della seconda dobbiamo impostare una "disequazione" dove
confronto le due offerte e vado a studiare quando la seconda è
maggiore della prima |
|
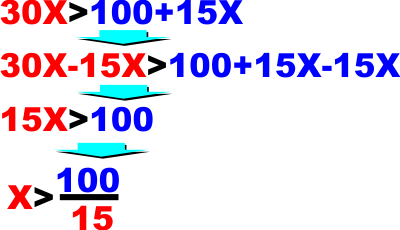 |
|
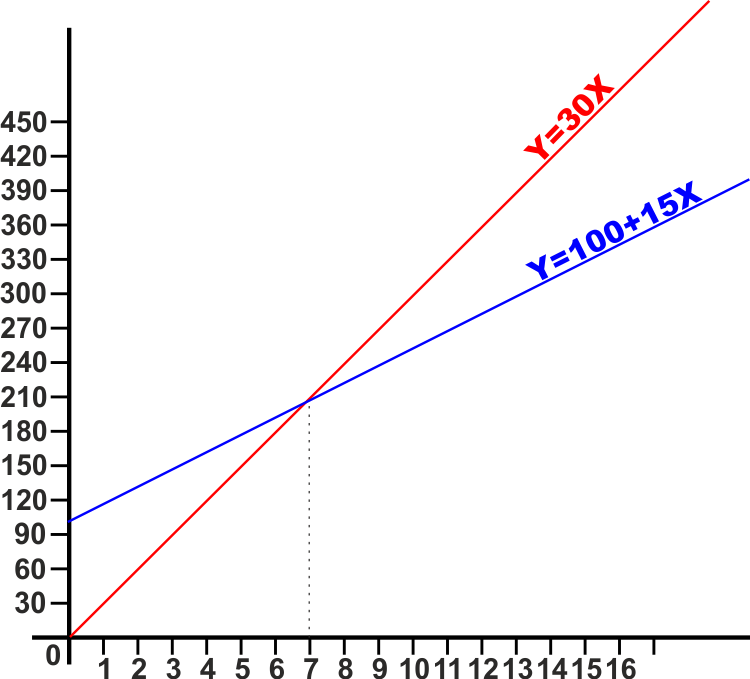
E abbiamo trovato questi 100/15 di giorno, che in pratica mi dice
che comincia a convenirmi l'abbonamento se scio almeno 7 giorni
(100/15 farebbe 6.66666 , ma ovviamente siccome qui pago a giorni
interi vuol dire che se scio per 6 giorni non mi conviene
l'abbonamento, dal settimo in poi - settimo compreso - si).
Se avessimo semplicemente risolto l'equazione imponendo
l'eguaglianza delle due funzioni (offerte), avremmo trovato lo
stesso valore, cioè avremmo saputo che al 100/15 esimo giorno, cioè
il 6,66666, le due offerte mi sarebbero costate identicamente, ma a
rigore questo non mi sarebbe bastato per sapere se dopo sarebbe
stata più conveniente l'una o l'altra. |
Se vogliamo "visualizzare" la disequazione, il modo più semplice è
quello di utilizzare il solito piano cartesiano.
Prendiamo una funzione qualsiasi (cioè una "legge matematica" che
lega le variabili y e x) .. la "disequazione" ci
indica per quali valori di X la funzione è maggiore di un certo
valore .. Per semplificarci la vita, facciamo finta di poter
scrivere la disequazione nella forma
f(x) > 0 . Ovviamente è sempre possibile (si tratta di
togliere tutto quello che c'è a destra e di conseguenza sottrarlo a
quello che c'è a sinistra del segno > ( o <) ...
In questo caso la nostra disequazione di fornirà i valori per i
quali la funzione, qualunque essa sia, è positiva.
Se la "funzione" è lineare, cioè una retta, la cosa è abbastanza
semplice ... La retta o sale sempre o scende sempre (non ha
massimi o minimi .. è retta) per cui sarà maggiore di zero per x più
grande ( o più piccola) di un certo valore e stop.
Ma se la funzione fosse più complicata? Ad esempio y = x2
- 9 ?
Sviluppandola ... vi ricordate i prodotti notevoli? x2
- 9 è come scrivere (x+3)(x-3) - se non ci credete fate
il conto.
Questa roba qui è positiva (maggiore di zero) in due casi .. cioè
sia che x+3 e x-3 siano ambedue positivi, sia che
x+3 e x-3 siano entrambi negativi.
Ricordate? + per + da +, - per - da +. |
 |
Per cui la cosa non è semplicissima ..
Anzi, pensate come sarebbe complicato se i termini fossero di più ..
Occorre fare ordine nei nostri pensieri e cercare di ridurre una
roba sulla quale ci perderemmo a ragionare a qualcosa di semplice ..
la più semplice possibile.
La più semplice possibile sarebbe ragionare solo sui due termini
semplici, nel nostro caso x+3 e x-3.
Quando è che questi sono positivi?
La cosa più semplice che mi viene in mente è di "visualizzare" la
soluzione.
per farlo mi traccio due righe, una interrotta sul valore -3 e
l'altra sul valore +3.
Poi vado a vedere quando ognuno dei due termini è positivo e ci
metto un segno + (ma posso scriverci qualsiasi cosa .. serve solo
per ricordarmi che li è positiva, se fossimo ancora alle elementari
che la farebbero colorare in blu o in nero) e un segno - dove è
negativa (o coloriamola in rosso) ...
Per sapere dove la nostra funzione è positiva basta vedere quando i
segni "meno" sono pari o dove non ce ne sono.
Negativa dove i segni meno sono dispari. |
E .. niente, basta così ... abbiamo un "metodo" per visualizzare il
comportamento di una funzione ( o se preferite per risolvere una
disequazione di ordine superiore al primo o un sistema di
disequazioni).
Prendiamo un caso più complesso, come esempio ...
Studiamo positività e negatività di una finzione dove ci siano
termini con la x al numeratore e con la x al denominatore ....
una roba tipo
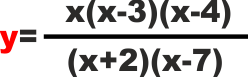
Qui abbiamo un mare di fattori diversi: x, (x-3) , (x-4) , (x+2)
, (x-7) ...
E allora?
Ripetiamo quanto abbiamo visto prima ... andiamo a vedere quando
sono positivi tutti i fattori, uno per uno ... |
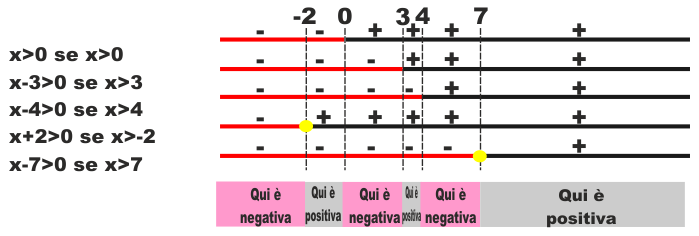 |
Rifacciamoci il nostro diagrammino e andiamo a vedere dove ogni
fattore è positivo o negativo.
Che i termini siano a numeratore o a denominatore non cambia nulla
(sul positivo e negativo, cambia sugli "zeri").
Quindi la funzione che abbiamo scritto lavora così:
è negativa per x<-2
non esiste per x=-2 (il denominatore avrebbe un fattore uguale a
zero e sappiamo che non si può dividere per zero)
è positiva per -2<x<0
vale 0 per x=0
è negativa per 0<x<3
vale 0 per x=3
è positiva per 3<x<4
vale 0 per x=4
è negativa per 4<x<7
non esiste per x=7 (il denominatore avrebbe un fattore uguale a zero
e sappiamo che non si può dividere per zero)
è positiva per x>7 |
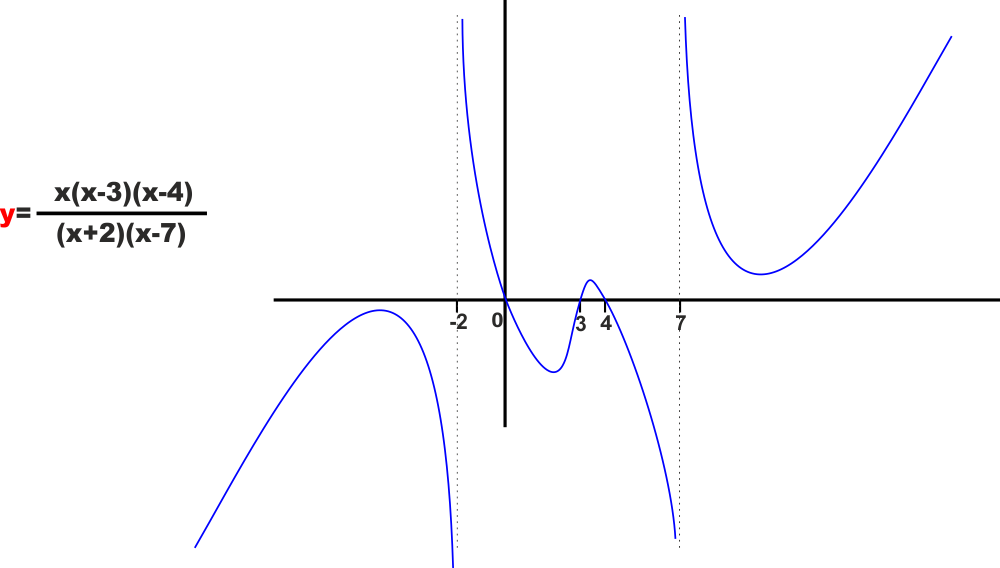
Se riportassimo la nostra funzione su un piano
cartesiano sarebbe una cosa del genere (figura a lato).
Come abbiamo visto, oltre a trovare dove è positiva e dove è
negativa, abbiamo trovato anche gli "zeri" della funzione
(che sono le soluzioni dell'equazione y=0) e due
"singolarità" che sarebbero i due valori di x per i quali la
funzione non può essere calcolata.
|
 |
|
Un "sistema" di disequazioni è invece un caso molto più semplice.
Si impongono due condizioni, non necessariamente concordi (nel senso
che devo andare a studiare solo se sono vere e non mi interessa se
sono ambedue del tipo x> di ... o una x>... e una x< ...), e si va a
studiare quando sono verificate entrambe.
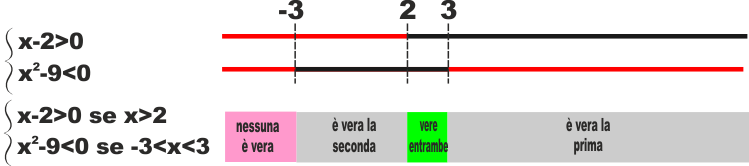
A lato vedete un esempio.
x-2>0 è vera se x>2
x2-9<0 lo abbiamo visto prima .. scomponiamo x2-9
e abbiamo (x+3)(x-3) .. qui ci si chiede quando è minore di zero e
quindi all'interno dell'intervallo -3<x<3 (fatevi i conti con la
tabellina che abbiamo visto prima).
A questo punto confrontiamo con una tabella simile le due soluzioni.
Qui non dobbiamo però studiare i segni, ma solo vedere dove sono
verificate entrambe le condizioni.
Vediamo che tutte e due le disequazioni sono vere solo per i valori
di x compresi tra 2 e 3. |
 |
|