1. Deve essere nulla la risultante di tutte le forze applicate a questo corpo
2. Deve essere nulla la somma dei momenti applicati a questo corpo.

Nel prossimo capitolo vedremo cosa vuol dire la seconda affermazione, per ora limitiamoci alla prima.

Intanto dobbiamo introdurre il concetto di "forza".
La definizione dinamica ed efficace la vedremo più avanti, quando parleremo dei tre principi della dinamica di Newton.
Per ora accontentiamoci di qualcosa di più intuitivo.
Parliamo di "tirare" un oggetto con una corda. Il concetto di "forza" è abbastanza semplice, è lo "sforzo" che dobbiamo fare per spostare, o anche solo sostenere, l'oggetto tirando il cavo.
Per quantificare la cosa, cioè per poter mettere dei numeri, sarà il caso di definire però almeno una "forza".
L'esempio più semplice che mi viene in mente è il "peso" di un corpo.
C'è differenza tra "massa" e "peso".
La "massa" (che misuriamo in kg) è una proprietà assoluta di un corpo. Per capirci, un litro d'acqua ha una "massa" di un kg.
Sulla Terra un litro d'acqua ha anche un "peso" di un kg, ma sono due cose decisamente diverse.
Sulla Luna la stessa quantità d'acque ha una massa sempre di un kg, mentre il "peso" sarebbe circa di 170 grammi.
Questo perché la "massa" è una grandezza che indica la quantità di materiale (diverso dal "volume", se un kg d'acqua si trasforma in vapore o in ghiaccio occupa un volume diverso, non più un litro, ma la sua massa resta di un kg), mentre il "peso" è una forza, dovuta all'interazione delle due "masse", quella dell'oggetto di cui parliamo e quella del pianeta su cui siamo.
La forza peso è sempre diretta verso il centro del pianeta (quindi banalmente per noi verso il basso) e vale (in Newton, che è l'unità di misura delle forze) mg cioè il prodotto della massa appunto, per la costante "g" che è l'accelerazione di gravità, che sulla Terra vale 9.8 m/s².

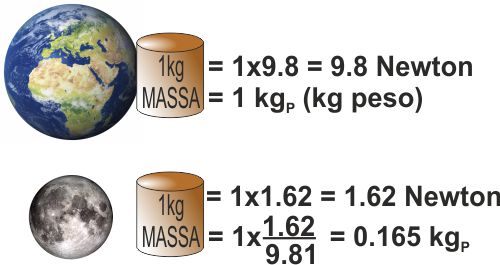
Per praticità, però, nel sistema "degli ingegneri", si confondono il kg massa (che è appunto una massa) col kg peso (che è una forza). Con questo sistema 1 kg massa corrisponde ad 1 kg peso. Negli esercizi e in genere per specificare senza ambiguità di cosa stiamo parlando, quando diciamo "un oggetto di massa 2 kg" intendiamo un oggetto che ha una massa di 2 kg e che quindi esercita una FORZA di 2x9.8 = 19.6 Newton. SE invece parliamo di un "oggetto del peso di 2 kg" intendiamo un aggetto che esercita una forza di 2 kg PESO (che sono sempre 19.6 Newton) diretta verso il basso. La massa resta la stessa ovunque ci troviamo, il peso dipende dalla forza di gravità, per cui varia se andiamo nello spazio o, come vedremo nella dispensa 8, anche sulla Terra in funzione della latitudine e della quota a cui ci troviamo.

EQUILIBRIO DELLE FORZE
Un corpo resta fermo (o permane nella sua condizione di moto rettilineo uniforme) se la risultante di tutte le forze ad esso applicate è nulla.
	La "risultante" è la somma VETTORIALE delle forze, che devono quindi essere viste come vettori, con un modulo, direzione e verso.

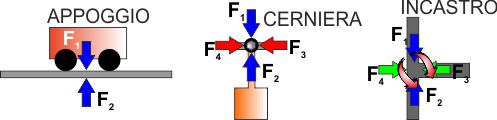
Le REAZIONI VINCOLARI Quando consideriamo un sistema dobbiamo analizzare come questo si collega al mondo esterno L'oggetto può essere APPOGGIATO su un piano, in questo caso il piano (se non vi è attrito) impedisce soltanto il movimento nella direzione normale (perpendicolare) a questo - l'oggetto è libero di spostarsi parallelamente al piano di appoggio. L'oggetto può essere INCERNIERATO (tipico collegamento con un bullone) - in questo caso non può muoversi ma può ruotare. L'oggetto può essere INCASTRATO (ad esempio con più bulloni o con saldatura) - in questo caso l'oggetto non può fare alcun tipo di movimento.

Le reazioni vincolari sono le forze messe in gioco dal vincolo, che sono solo una "reazione" alle altre forze cha agiscono sul sistema, ad esempio nella figura il carrello appoggiato che pesa F₁ sarà sostenuto da una reazione vincolare F₂ in direzione e modulo uguale ad F₁ ma di verso opposto (più semplicemente opposta ad F₁)
 

ESERCIZIO DI ESEMPIO

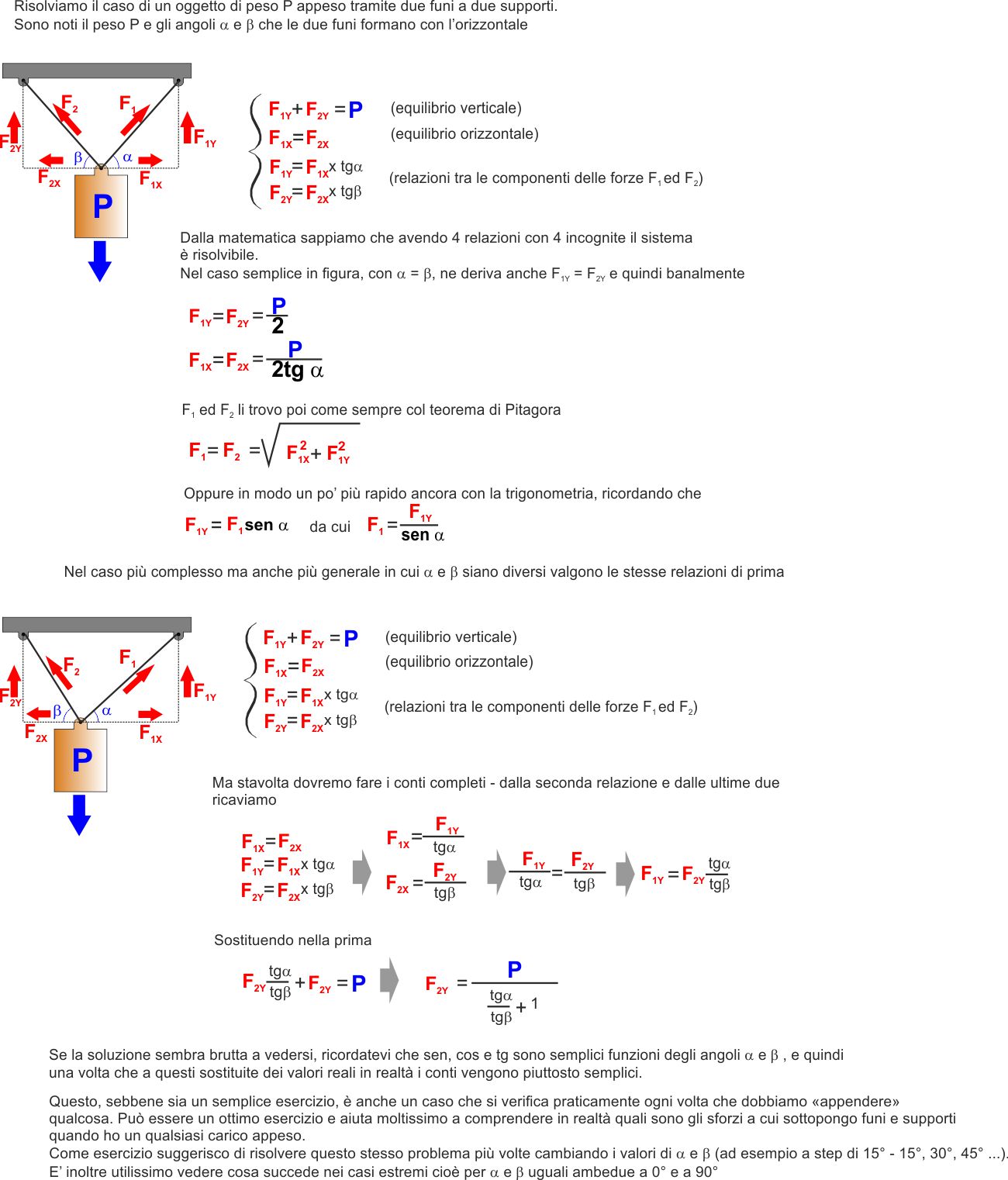
ESERCIZIO DI ESEMPIO

LA FORZA DI ATTRITO

• ATTRITO STATICO - Che si esercita tra due superfici FERME a contatto tra loro
• ATTRITO RADENTE  - Che si esercita tra due superfici a contatto tra loro ma in movimento reciproco (strisciano l'una sull'altra)
• ATTRITO VOLVENTE - Che si esercita tra una superficie ed una corpo che ci "rotola" sopra (le ruote dell'auto sull'asfalto).

 Nella formulazione classica, dovuta a Coloumb, si identifica un numero detto "coefficiente di attrito" che si indica con la lettera greca μ (si legge mu) e vale la formula
 

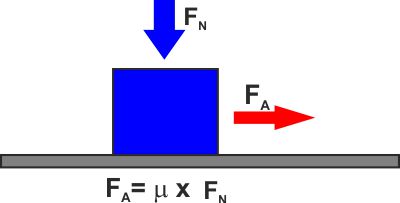
con μ indipendente dalla velocità, dall'estensione della superficie di contatto.
 

In realtà queste ipotesi non si sono dimostrate rigorosamente corrette, ma per quanto interessa noi, che per ora ci occuperemo solo della condizione di attrito statico, l'attrito "coloumbiano" è una approssimazione lecita e funzionale del fenomeno. Per i nostri esercizi la differenza rispetto a problemi come quelli visti prima è che qui le due forze "normali" (cioè perpendicolari tra loro) non sono più indipendenti, ma c'è una relazione che le lega. Parlando di attrito dobbiamo sempre considerare che la forza si oppone ad un tentativo di muovere l'oggetto, pertanto il valore FA = μFN è un valore MASSIMO. Se lo si supera il corpo si muove, sino a che invece si esercita una forza di intensità inferiore il corpo resta fermo. Nella tabella a lato ho raccolto alcuni esempi di coefficienti d'attrito tra materiali di uso comune.
I pneumatici delle auto di F1 hanno coefficienti d'attrito superiori ad 1 - rientrano praticamente nel campo delle colle.

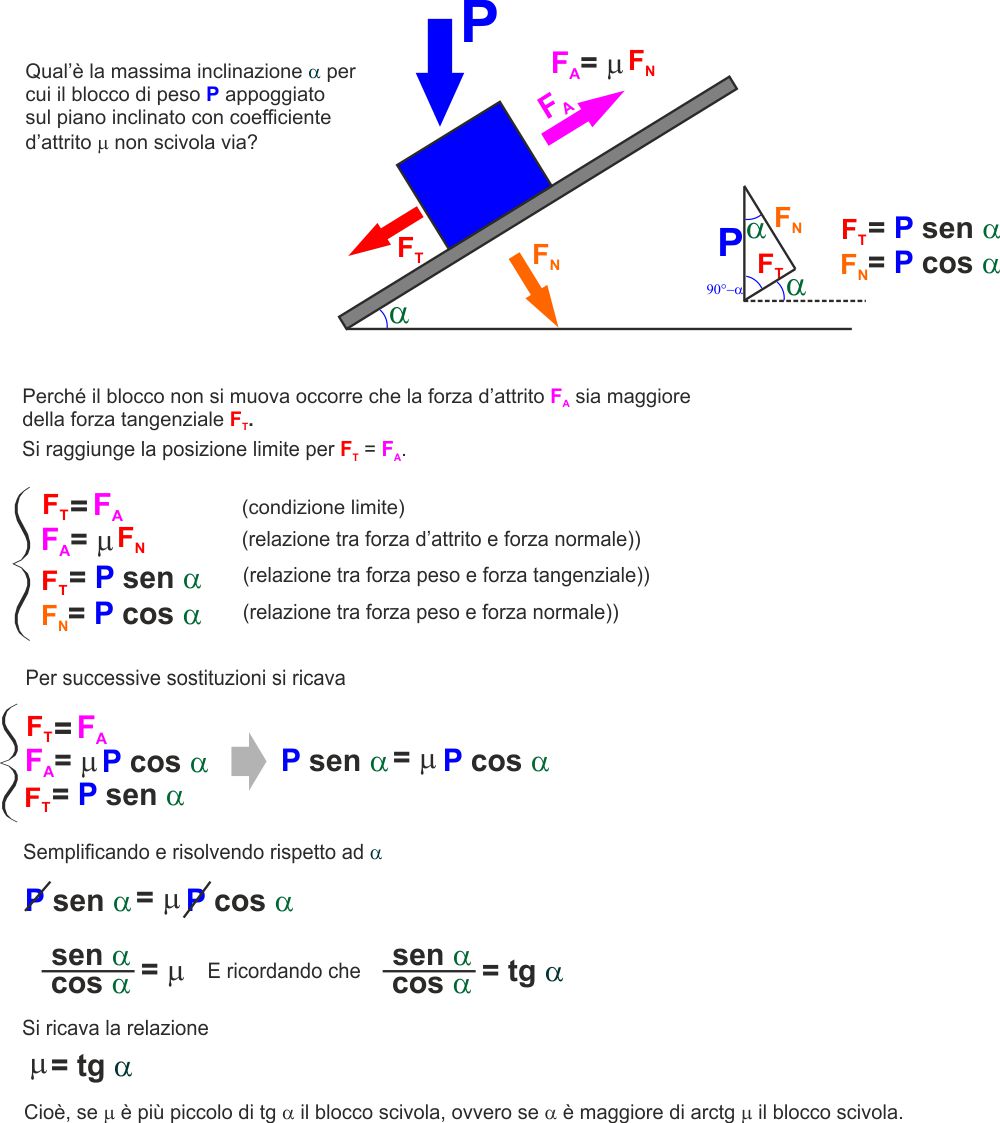
ATTRITO SU UN PIANO INCLINATO