Sino ad ora abbiamo visto solo dimostrazioni di tipo diretto.
In questo capitolo faremo uso anche di dimostrazioni "indirette", o,
per assurdo.
Attenzione.
Sebbene quello che facciamo sia rivolto alla geometria, in realtà il
modo di ragionare rigoroso (e non "rigido", che suona male) si può
(e si dovrebbe) applicare a qualsiasi tema si stia affrontando.
Ed è proprio, ricordo, questo lo scopo per cui nasce nell'antica
Grecia.
Quindi non solo possiamo ragionare dimostrando che necessariamente
una certa ipotesi giustifica una certa tesi, ma possiamo anche
ragionare all'opposto.
Partiamo dall'ipotesi e NEGHIAMO la tesi.
Andiamo poi a vedere che se le cose fossero così (cioè al contrario
di quello che vogliamo dimostrare) si cadrebbe in una assurdo (cioè
il ragionamento porta a qualcosa di impossibile o evidentemente
sbagliato. |
 |
Vi faccio un esempio semplice e disgiunto dalla
matematica. Mi piacerebbe che servisse per capire la differenza tra
un ragionamento fatto col cervello e un'affermazione "buttata li".
Domanda:
"Perché il cielo è azzurro?".
Alcuni di voi lo sanno, altri ci ragionano su .. ma tutte le volte
che ho posto questo quesito in classe qualcuno ha risposto:
"PERCHE' RIFLETTE IL COLORE DEL MARE" .
Fermatevi un attimo su questa affermazione e immaginate, per un
secondo, che sia vera.
Cosa comporterebbe?
Banale: dove il mare non si vede (tipo a Milano) il cielo dovrebbe
essere color "tetti di Milano" .
Su un bosco? Verde foglia ...
Sul deserto? Color sabbia ..
Quindi anche se non vi dico perché il cielo è azzurro (dipende
dall'assorbimento delle radiazioni solari da parte delle molecole di
O2 nell'atmosfera, ma non è questo il punto) vi ho
dimostrato che l'affermazione comporterebbe conseguenze assurde, e
quindi sicuramente non è vera.
Nello stesso modo possiamo ragionare anche in geometria, e ora ne
vediamo un esempio. |
|
 |
TEOREMA : Due rette parallele ad una terza sono parallele tra di
loro. IPOTESI: la retta a
è parallela alla retta b e anche
la retta c è parallela alla
retta b
TESI : la retta a è parallela
alla retta c
Dimostrazione: Ragioniamo per assurdo: le rette, abbiamo visto,
possono essere solo o parallele o incidenti. Se sono parallele non
sono incidenti e viceversa (escludiamo il caso di rette coincidenti
perché se due o più delle rette fossero coincidenti sarebbero la
stessa retta e il teorema sarebbe già dimostrato).
Quindi se le rette a e
c non fossero parallele vorrebbe
dire che avrebbero almeno un punto P in comune.
Questo vorrebbe dire che per il punto P passerebbero due
rette distinte (a e
c), ambedue (per ipotesi) parallele
alla retta b.
Ma questo contraddice il quinto postulato di Euclide, secondo il
quale per un punto esterno ad una retta passa una ed una sola retta
a questa parallela.
|
|
Quindi se a e
c non sono parallele tra di loro
non possono nemmeno essere tutte e due parallele a
b.
Abbiamo quindi dimostrato che a e c sono parallele (come volevamo)
perché se non lo fossero non potrebbero nemmeno essere tutte e due
parallele a b, che era
l'ipotesi.
TEOREMA: Se due rette sono parallele ogni retta incidente ad una
è incidente anche all'altra.
Ipotesi Sono date due rette c
e b parallele tra loro e una
retta a che ha in comune con la
retta c un punto (cioè che
interseca la retta c).
Tesi : Vogliamo dimostrare che la retta
a interseca anche la retta b.
Ragioniamo per assurdo: Se a
e b non si intersecassero,
sarebbero parallele. E quindi, per il teorema che abbiamo appena
dimostrato anche a e
c dovrebbero essere parallele, e
quindi non possono intersecarsi in P. |
 |
|
RETTE TAGLIATE DA UNA TRASVERSALE |
Quando due rette a e b intersecano una terza retta c in
due punti distinti, formano con questa 8 angoli, che
prendono nomi particolari (che occorre imparare a memoria
perché sono "definizioni"). Con riferimento alla figura a
lato::
- Gli angoli che stanno tra le due
rette a e b sono "interni"
- Gli angoli che stanno "fuori"
rispetto alle due rette a e b si chiamano "esterni"
- Quelli che stanno dalla stesa parte
rispetto alla retta c si chiamano "coniugati"
- Quelli che stanno da parti opposte
rispetto alla retta c si dicono "alterni"
- Gli angoli coniugati che sono uno
esterno e uno interno si chiamano "corrispondenti"
Nota a parte:
Per favore andatevi a vedere come si
pronunciano le lettere
greche, che male non fa. |
 |
 |
TEOREMA: Se (IPOTESI)
due rette tagliate da una trasversale formano:
- o due angoli alterni
interni uguali
- o due angoli alterni
esterni uguali
- o due angoli corrispondenti
uguali
- o due angoli coniugati
interni supplementari
- o due angoli coniugati
esterni supplementari
allora (TESI) saranno uguali
anche tutte le coppie di angoli alterni interni,alterni
esterni e corrispondenti, e saranno supplementari tutte le
coppie di angoli coniugati esterni e coniugati interni.
|
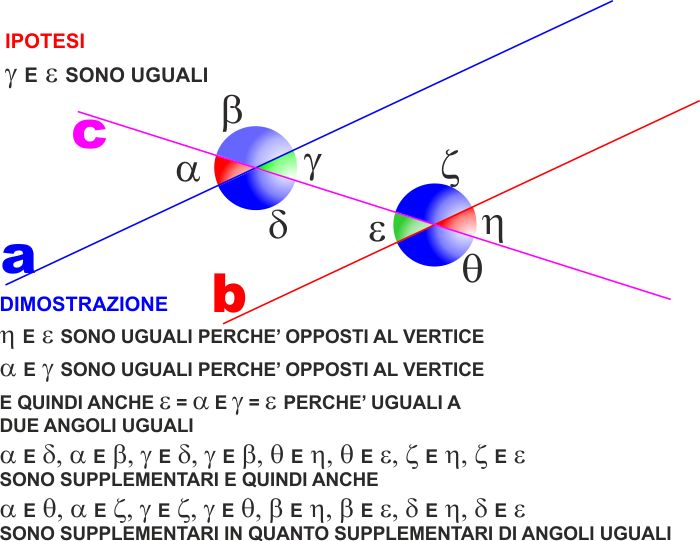
Dimostriamo un solo caso, e come esercizio
dimostrate, in modo analogo, gli altri.
Se (ipotesi) i due angoli alterni interni
γ
e
ε
sono uguali, allora:
-
α
= γ
perché opposti al vertice
-
ε
=
η
perché opposti al vertice
e quindi anche
α
=
η
perché uguali ad angoli uguali.
- γ
e
δ
sono supplementari
- γ
e
β
sono supplementari
-
ε
e
ζ
sono supplementari
-
ε
e
θ
sono supplementari
e quindi (tesi) anche
β, δ, ζ, θ
sono uguali perché
supplementari di angoli uguali
così come (sempre tesi):
-
ε
e
δ
sono supplementari
-
ε
e
β
sono supplementari
-
α
e
ζ
sono supplementari
-
α
e
θ
sono supplementari
-
η
e
δ
sono supplementari
-
η
e
β
sono supplementari
- γ
e
ζ
sono supplementari
- γ
e
θ
sono supplementari
perché anche qui supplementari di angoli uguali |
 |
|
|
CRITERI DI PARALLELISMO DI DUE RETTE |
Eccoci finalmente al "succo" del capitolo.
Ancora un paio di dimostrazioni e avremo in mano gli
strumenti per poter dire se due rette sono o meno parallele. |
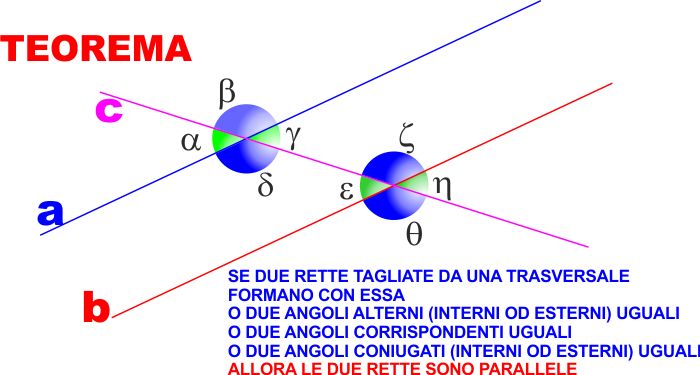
TEOREMA: Se due rette
tagliate da una trasversale formano con questa :
- due angoli alterni (interno
o esterni) uguali o
- due angoli corrispondenti
uguali o
- due angoli coniugati
(interni o esterni) supplementari
allora
le due rette sono parallele
IPOTESI: Due rette a e b formano
con la retta c due angoli alterni interni uguali
(basta dimostrare questo caso in quanto abbiamo appena
dimostrato che tutte le altre ipotesi indicate sopra
comportano necessariamente i due angoli alterni interni
uguali .. e anche tutto il resto, come abbiamo visto nel
paragrafo precedente)
TESI : Le due rette sono
parallele
DIMOSTRAZIONE:
Ragioniamo per assurdo, se a e b non fossero parallele
dovrebbero avere un punto P in comune e quindi detti A e B i
punti di intersezione con la retta c avremmo un triangolo
ABP che avrebbe (per i teoremi visti prima) i due angoli in
A e in B complementari.
Cioè l'angolo in B sarebbe uguale all'angolo esterno in A,
in contraddizione col teorema visto al capitolo precedente
che vuole che ogni angolo esterno sia maggiore di ognuno dei
due angoli interni non adiacenti.
Non potendo avere punti in comune (cioè non potendo formare
un triangolo) le due rette a e b devono per forza essere
parallele
|
 |
|
|
|
 |
TEOREMA (inverso del precedente):
Se due rette sono parallele, allora tagliate da
una trasversale formano con essa formano:
-
angoli alterni (sia interni
che esterni) uguali
-
angoli corrispondenti
uguali
-
angoli coniugati
(sia interni che esterni) supplementari
IPOTESI: Due rette a e b
sono parallele
TESI :
Dobbiamo dimostrare che li angoli alterni interni
γ
e
ε
sono uguali
DIMOSTRAZIONE: Anche qui ragioniamo
per assurdo e supponiamo quindi che i due angoli siano
diversi.
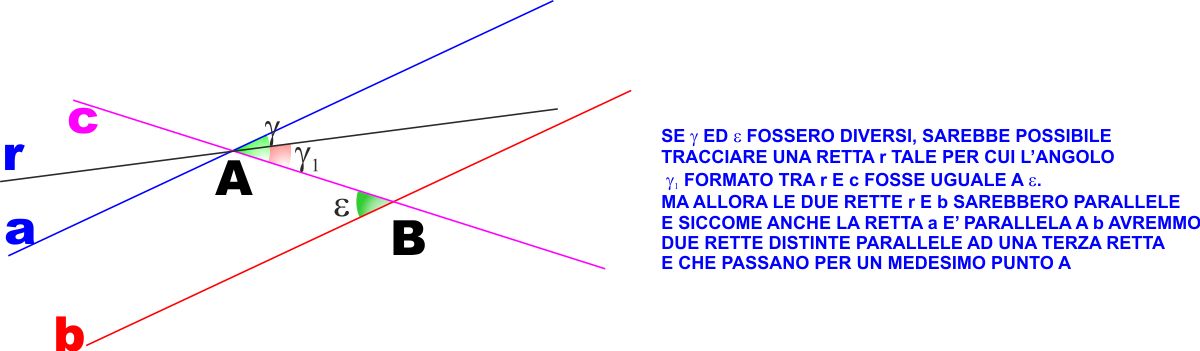
Se fossero diversi sarebbe possibile tracciare una ulteriore
retta r che passi per A e che formi con c
un angolo
γ1
diverso da
γ
ma uguale a
ε.
Se lo facessimo, per il teorema precedente le rette r e b
dovrebbero essere parallele.
Ma allora, visto che per ipotesi la retta a è
parallela alla retta b e passa per A, avremmo
due rette distinte a ed r, ambedue parallele a
b che passerebbero per A, e questo è assurdo. |
 |
|
TEOREMA FONDAMENTALE SULLE RETTE
PARALLELE:
Condizione necessaria e sufficiente
affinché due rette siano parallele è che, tagliate da una trasversale
formino :
-
angoli alterni (sia interni
che esterni) uguali o
-
angoli corrispondenti
uguali o
-
angoli coniugati
(sia interni che esterni) supplementari
|
 |
|
I seguenti corollari provate prima a dimostrarli da soli e
solo successivamente leggete le dimostrazioni.: |
 |
COROLLARIO 1:
Se due rette sono parallele anche ogni retta
perpendicolare ad una delle due è perpendicolare anche all'altra.
IPOTESI : Le rette a e b sono parallele e la retta c è
perpendicolare ad a
TESI: La retta c è
perpendicolare anche a b
DIMOSTRAZIONE: Per il teorema fondamentale sulle
rette parallele gli angoli (ad esempio) alterni interni
γ
e
ε
formati con la trasversale c sono uguali e quindi se uno è retto anche
l'altro deve esserlo, pertanto c è perpendicolare a tutte e due. |
|
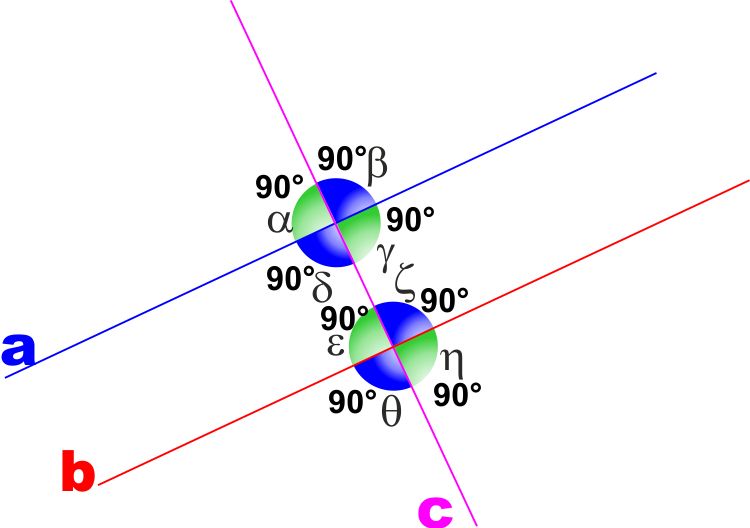
COROLLARIO 2:
Due rette sono
perpendicolari ad una terza sono tra
loro parallele
IPOTESI : Le rette a e b sono ambedue perpendicolari
alla retta c
TESI: Le rette a e b sono
parallele
DIMOSTRAZIONE: Per ipotesi gli angoli (ad esempio)
alterni interni
γ
e
ε
formati dalle due rette a e b la trasversale c sono retti e quindi
sono uguali.
Di conseguenza, per il teorema fondamentale sulle rette parallele a e b sono
parallele perché formano con c angoli alterni interni uguali. |
|
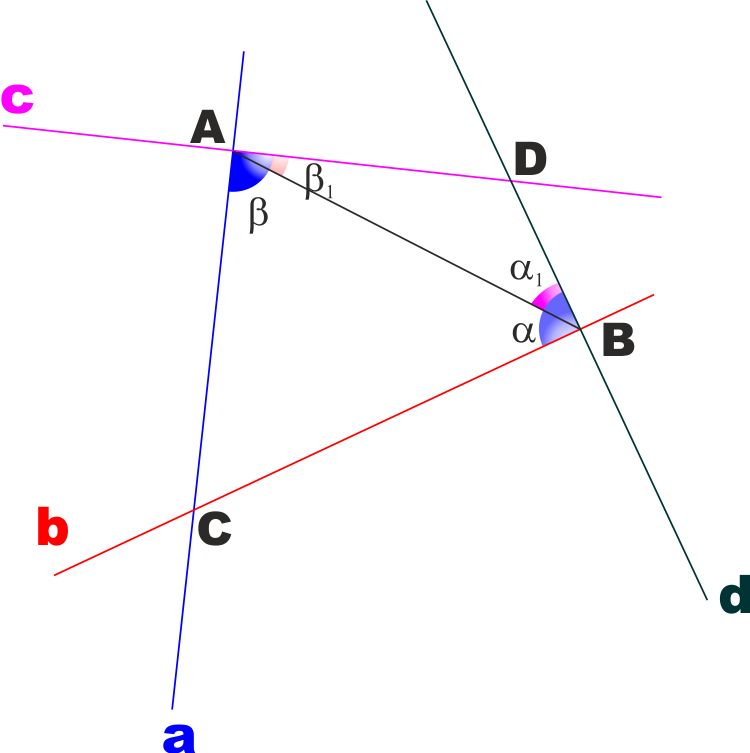
COROLLARIO 3:
Le perpendicolari a due rette incidenti sono
anch'esse incidenti
IPOTESI : Le rette a e b
sono incidenti (non sono parallele)
e le rette c e d sono perpendicolari
rispettivamente ad a e a b
TESI: Le rette c e d sono
incidenti (non sono parallele)
DIMOSTRAZIONE: Le due rette a e b sono
incidenti in C, mentre le due perpendicolari c e d sono
incidenti rispettivamente ad a in A e a b in B.
Con riferimento alla figura a lato, se io traccio il segmento AB
(unendo i punti A e B) questo forma con le rette c e
d due angoli
α1
e β1
che sono interni ai due angoli retti
α
e β
.
Essendo α
e β
retti gli angoli
α1
e β1
sono più piccoli di due angoli retti e di conseguenza la loro somma non è un
angolo piatto, cioè non sono supplementari.
Allora le rette c e d non sono parallele in quanto hanno due
angoli corrispondenti non supplementari.
|
 |
|
|















