|
||||||||
| La navigazione astronomica è ormai da anni inutilizzata. Chiunque voglia calcolare il punto nave sarebbe un pazzo a portarsi dietro un sestante (valore oltre i 6.000.000 di lire) e una edizione aggiornata delle effemeridi (le tavole dove si trovano i dati indispensabili per eseguire i calcoli di navigazione astronomica valore circa 100.000 lire, ingombro cm 30x25x4), piuttosto che un "comune" GPS (costo inferiore a 800.000 lire) il quale senza alcun calcolo è in grado di fornire con precisione di alcuni metri non solo la posizione, ma anche indicazioni in tempo reale di rotta, velocità, quota, e quant'altro il più o meno sofisticato software di cui l'apparecchietto fosse dotato fosse in grado di indicare (senza spendere capitali si possono facilmente reperire GPS in grado di visualizzare su un cartina digitalizzata direttamente sul display il punto nave e quindi di seguire una rotta anche composta da più tratte spezzate). | ||||||||
|
|
Resta però il fascino di sapere
come facevano gli antichi navigatori che non solo non disponevano di GPS,
ma neanche di radiogoniometro o ecoscandaglio o anche della semplice
bussola (importata dalla Cina in tempi relativamente recenti). |
|||||||
|
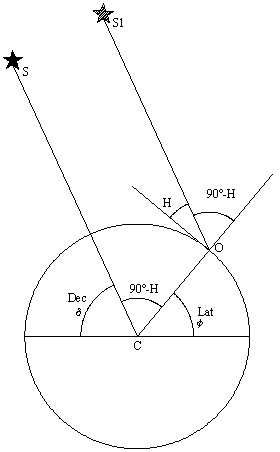
Nella figura in particolare si osserva che se la stella S è
esattamente al Nord (la Stella Polare), essendo le rette C (centro
della Terra) - S e O - S1 parallele, i due angoli
complementari dell'altezza misurata H e della latitudine f
(90°-H) sono uguali da cui discende che l'altezza misurata H della
stella Polare è proprio uguale alla latitudine dell'osservatore. |
||||||||
| E gli antichi ben così
navigavano:
Erano in grado di trovare con precisione solo la latitudine (non con la Polare, perché in effetti non è, purtroppo, esattamente al Nord), e quindi navigavano per paralleli. Ad es., se Cristoforo Colombo voleva arrivare a Santo Domingo (circa 18° Lat. Nord) e si trovava nelle Azzorre (circa 38° Lat Nord), non faceva altro che scendere di latitudine sino ad incrociare il 18° parallelo e quindi proseguiva mantenendosi su questo fino a ritrovarsi a Santo Domingo. Ovviamente il metodo era funzionale ma non certo praticissimo. Ben lungi da seguire la rotta più breve (e sfido anche il più esperto dei nostri naviganti a calcolarla, se rinuncia a tutto quanto consegue la nozione acquisita che la terra è sferica), il buon Cristoforo era però certo che prima o poi sarebbe arrivato a destinazione, e all'epoca non era poco. |
|
|||||||
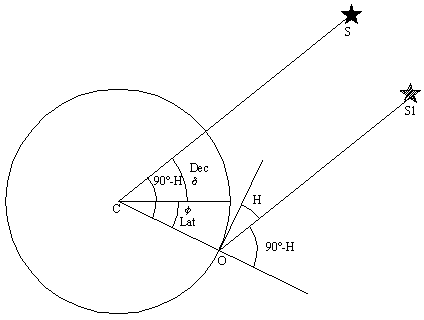
| Come già detto non è con la Polare che si poteva trovare con precisione la latitudine, ma con qualunque stella (compreso il sole) di cui fosse nota la declinazione d, aspettandone il passaggio allo Zenit, l'operazione non era poi più di tanto difficoltosa. | ||||||||
|
Osservando di volta in volta le figure di vede che la latitudine f si trova con semplici somme e sottrazioni di angoli: I caso (sopra): f = 90°+H+d II caso (a fianco): f = 180°-(90°-H)-d = 90° + H - d III caso (sotto): f = 90°- H - d (in questo caso è Lat Sud) |
|||||||
|
|
||||||||
|
Resta da spiegare due punti:
La declinazione delle stelle d è
fissa (o almeno varia molto lentamente a causa della precessione degli
equinozi) e corrisponde alla loro latitudine (sulla sfera celeste anziché
sulla Terra) per cui non è necessario portarsi dietro un librone ma solo
alcuni appunti che ne riportino il valore per qualche stella (un ventina,
disperse alle varie latitudini, sono più che sufficienti).
|
||||||||