|
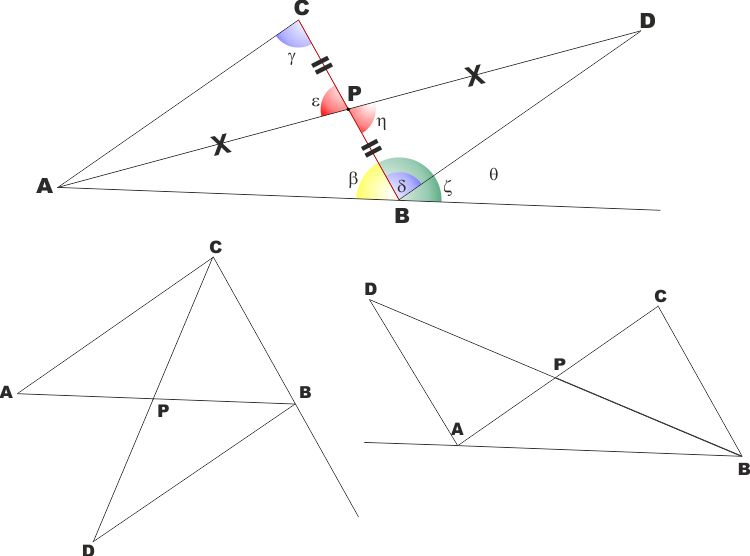
TEOREMA: In un triangolo qualsiasi angolo esterno è maggiore di
ciascuno dei due angoli interni non adiacenti.
IPOTESI: ABC è un
triangolo su cui non si fa alcuna ipotesi (quindi nessuna particolare
relazione tra i lati o tra gli angoli)
TESI: L'angolo esterno in B
(ζ)
è maggiore dell'angolo interno in C(γ)
e dell'angolo interno in A.
DIMOSTRAZIONE: Sia ABC un triangolo qualsiasi
(che vuol dire che non è necessariamente rettangolo o isoscele o equilatero,
ma che potrebbe anche esserlo senza che ciò cambi il senso della
dimostrazione).
Vogliamo dimostrare che preso uno qualsiasi dei tre angoli esterni, questo è
maggiore di ciascuno degli altri due angoli interni.
Facciamo la dimostrazione come in figura a lato, nel caso dell'angolo in
B e dimostrando che l'angolo esterno in B è maggiore dell'angolo
interno in C, ma la stessa dimostrazione si può applicare allo
stesso angolo B per dimostrare che il suo esterno è maggiore
dell'angolo interno in A.
Prolunghiamo il lato AB e valutiamo quindi l'angolo esterno ζ
costruito su questo prolungamento.
Dividiamo il lato CB in due parti uguali e sia P il punto
medio di CB. Tracciamo il segmento AP e prolunghiamo con un
altro segmento PD = AP.
I triangoli ACP e PBD sono uguali perché:
-
i due angoli in P (
ε
e η
) sono uguali perché opposti al vertice
-
i lati CP e PB sono uguali per costruzione
-
i lati AP e PD sono uguali per costruzione
I due triangoli sono uguali perché hanno due lati e l'angolo
tra essi compreso uguali.
Quindi anche l'angolo in C ( γ
) è uguale all'angolo in B (
δ
).
Come si vede dalla figura
δ
è interno all'angolo
ζ
e quindi è più piccolo, come volevamo dimostrare.
Possiamo ripetere la dimostrazione rifacendo costruzioni a
considerazioni analoghe per gli altri angoli - si lasciano tali
dimostrazioni come esercizio. |