|
PROIEZIONI |
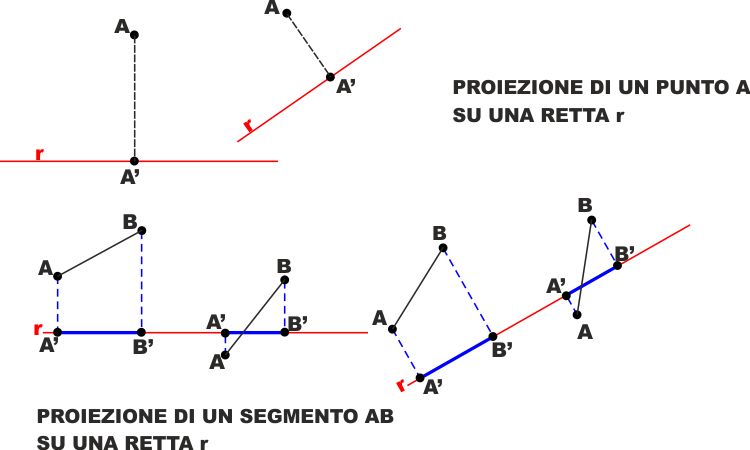
| Cominciamo con dare delle DEFINIZIONI: Si dice
PROIEZIONE DI UN PUNTO A su una retta r
il piede A' della retta perpendicolare a r condotta da A.
Si dice PROIEZIONE DI UN SEGMENTO AB
su una retta r il segmento A'B' che ha per estremi i punti A'B'
proiezioni dei due punti A e B estremi da AB sulla retta r. |
 |
| Date queste definizioni dimostriamo un importante teorema :
TEOREMA: Il segmento perpendicolare
condotto da un punto ad una retta è il minore tra tutti i segmenti
obliqui condotti dallo stesso punto alla medesima retta.
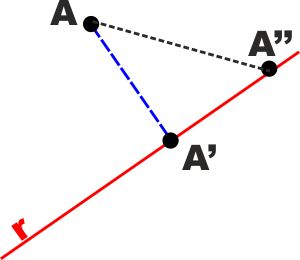
DIMOSTRAZIONE :
Consideriamo il triangolo AA'A'', è un triangolo rettangolo
perché per ipotesi AA' è perpendicolare a r (A'A'').
Quindi l'angolo in A' è sicuramente maggiore di ciascuno degli altri
due e di conseguenza anche il segmento AA' opposto all'angolo in A'
è maggiore di ciascuno degli altri due (in un triangolo ad angolo
maggiore sta opposto lato maggiore)
E già che ci siamo facciamo questa osservazione:
COROLLARIO: In un triangolo
rettangolo l'ipotenusa è sempre maggiore di ciascuno dei due cateti.
|
 |
Ne deriva una FONDAMENTALE DEFINIZIONE:
Il segmento di perpendicolare condotto da un punto ad una retta
si chiama DISTANZA DEL PUNTO DALLA RETTA. |
| |
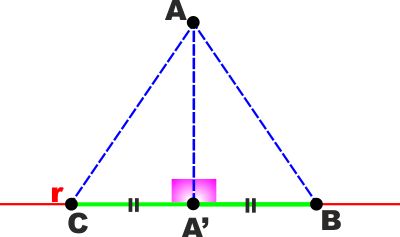
TEOREMA: Due segmenti obliqui condotti da un
punto ad una retta ed aventi su questa proiezioni uguali sono
uguali.IPOTESI:
AB è un segmento obliquo portato dal punto A
sulla retta r e A'B è la sua proiezione su r.
AC è un qualsiasi segmento portato da A ad r ed è A'C=A'B
TESI: AB e AC sono uguali.
DIMOSTRAZIONE:
(prima di leggerla però provateci da soli)
I triangoli AA'B e AA'C hanno:
AA' in comune
L'angolo in A' retto per ipotesi e quindi uguale
A'B=A'C per ipotesi
Sono quindi uguali e di conseguenza anche i lati AB e AC sono uguali
come volevamo dimostrare. |
 |
|
|
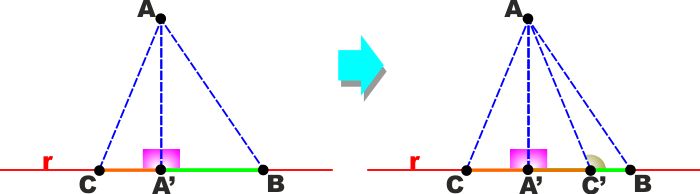
TEOREMA: Due segmenti obliqui condotti
da un punto ad una retta ed aventi su questa proiezioni diseguali
sono diseguali e a proiezione maggiore corrisponde segmento obliquo
(detto anche semplicemente OBLIQUA) maggiore. IPOTESI:
AB è un segmento obliquo portato dal punto A
sulla retta r e A'B è la sua proiezione su r.
AC è un qualsiasi segmento portato da A ad r ed è A'C<A'B
TESI: AB e AC sono diseguali e AC<AB
DIMOSTRAZIONE:
Se A'C<A'B è possibile riportare su AB il punto C' tale che A'C'
= A'C.
Siccome AA'C è rettangolo, sicuramente l'angolo in C' di questo è
acuto, di conseguenza il suo angolo esterno sarà ottuso.
Quindi nel triangolo AC'B l'angolo in C' è ottuso e quindi è
maggiore di ciascuno degli altri due.
Ne consegue che AC'<AB, opposto all'angolo maggiore, come volevamo
dimostrare.
|
|
LUOGHI GEOMETRICI E ASSE DI UN SEGMENTO |
Diamo questa importante definizione:
Si dice LUOGO GEOMETRICO o
semplicemente LUOGO una figura per la quale è stata enunciata
una certa proprietà di cui godano tutti i suoi punti ed essi
soltanto.
A semplice esempio citiamo qui alcuni noti "luoghi geometrici",
anche se ne studieremo le proprietà più avanti.

|
| DEFINIZIONE: Si dice ASSE di UN
SEGMENTO la perpendicolare al segmento condotta per il
suo punto medio. TEOREMA: L'asse
di un segmento è il luogo geometrico dei punti equidistanti dai suoi
estremi.
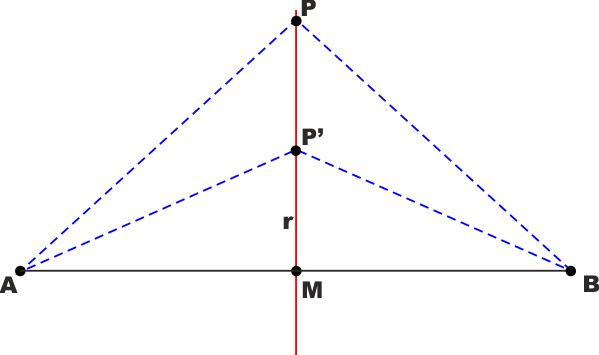
DIMOSTRAZIONE: Abbiamo detto per ipotesi che M è il punto
medio di AB e che r è perpendicolare ad AB.
Allora tutti i segmenti condotti da un qualsiasi punto P .. P' di r
ad A e a B sono le "oblique" delle proiezioni MA e MB, uguali per
ipotesi.
Quindi anche tutti i segmenti PA sono uguali ai segmenti PB comunque
su scelga P su r.
In questo modo abbiamo dimostrato che TUTTI i punti di r sono
equidistanti da A e B
In realtà questo non basta, dobbiamo anche dimostrare che se AP =
PB il punto P appartiene a r.
Cioè dobbiamo dimostrare anche che TUTTI i punti equidistanti da A e
da B appartengono alla retta r.
Lo dimostriamo osservando che il triangolo APB è isoscele (questa
volta AP=PB per ipotesi) e di conseguenza la retta r che è mediana
del lato AB è anche altezza di APB e quindi passa per P.
Ne consegue che se due rette sono
simmetriche rispetto ad un asse r il punto P di intersezione tra una
retta e l'asse è anche punto di intersezione tra l'altra retta e lo
stesso asse. |
 |
|
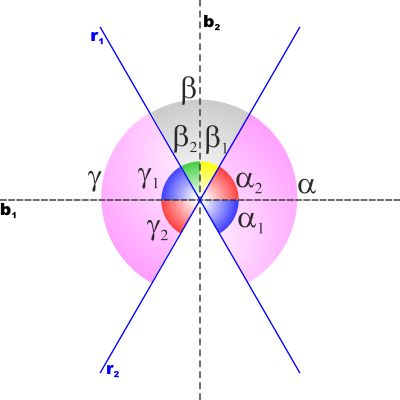 |
TEOREMA: Le semirette bisettrici
dei quattro angoli formati da due rette incidenti sono a due a due
in linea retta e perpendicolari
Siano r1 ed r2 due rette incidenti.
Consideriamo inizialmente i due angoli
α e γ
, vogliamo dimostrare che le due bisettrici dei
α e γ
sono allineate (cioè sono la stessa retta).
Tracciamo quindi la bisettrice del solo angolo
α e
prolunghiamola. Ci basterà dimostrare che gli angoli γ1
e γ2
che forma con le rette r1 ed r2 sono uguali e
quindi che è la bisettrice anche dell'angolo γ.
Basta osservare che γ1
e
α1
sono uguali perché opposti al vertice, così come γ2
e
α2.
Pertanto essendo
α1=α2
anche γ1=γ2
e siccome la loro somma è γ
abbiamo dimostrato che r1 è anche bisettrice di γ,
e che quindi le bisettrici di due angoli opposti al vertice sono
allineate.
Ora dobbiamo dimostrare che b2 è perpendicolare a b1
.
Possiamo lavorare così:
α e β
sono supplementari cioè la loro somma è un angolo piatto.
Ma β1
e
α2
sono la metà di β
e di a e quindi siccome
α/2+β/2
è uguale a (α+β)/2
e cioè alla metà di un angolo piatto anche β1+α2
è la metà di un angolo piatto, cioè un angolo retto.
Quindi b1 e b2 sono tra loro perpendicolari. |
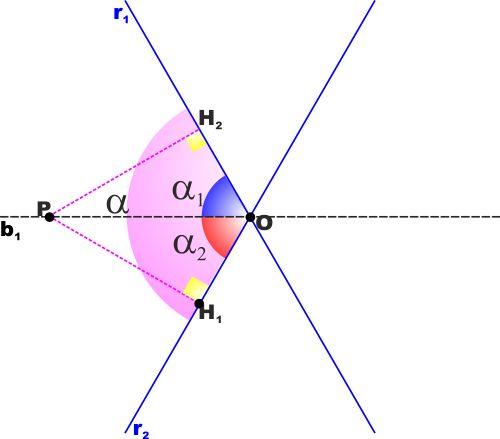
| TEOREMA: Il luogo geometrico dei
punti equidistanti da due rette incidenti sono le bisettrici degli
angoli formati da queste rette. Lo dimostriamo solo per
una bisettrice, la stessa dimostrazione vale ovviamente anche per
l'altra.
Cominciamo col dimostrare che PH1=PH2 e
cioè che tutti i punti che stanno sulla bisettrice b1
sono equidistanti dalle due rette r1 ed r2.
PH2O e PH1O sono uguali in quanto hanno:
PO in comune
L'angolo in O uguale per ipotesi (b1 è la bisettrice)
Sono ambedue rettangoli.
Sono quindi uguali per il criterio generale di uguaglianza dei
triangoli rettangoli (hanno anche un lato e un angolo uguali)
Quindi Tutti i punti che stanno sulla bisettrice sono equidistanti
dalle due rette.
Ora resta da dimostrare che se un punto è equidistante dalle due
rette sta anche sulla bisettrice.
Ipotizziamo ora che PH1 si uguale a PH2
i triangoli PH2O e PH1O sono di nuovo uguali
in quanto hanno:
AO in comune
PH2=PH1 per ipotesi
Sono quindi due triangoli rettangoli che hanno uguali l'ipotenusa e
un cateto, e sono quindi uguali.
Come volevamo dimostrare.
|
 |
| |
|
|
POLIGONI |
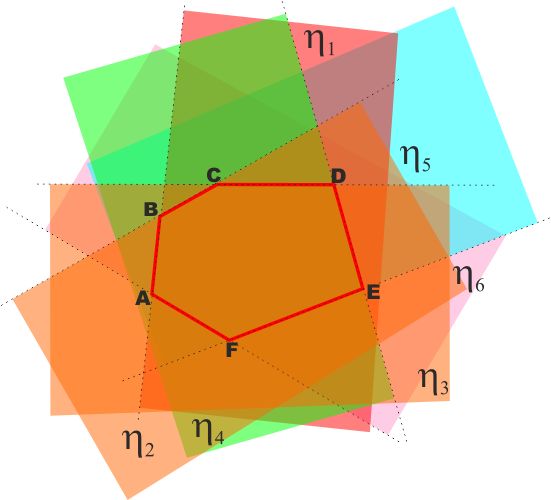
Sia ABCDEF.... una poligonale chiusa tale che, considerati due
suoi vertici qualsiasi consecutivi (ad es. A e B) tutti i restanti
vertici (C,D,F...) appartengono ad uno solo dei due semipiani di
origine AB.
Indicato con η1
tale semipiano e con η2
quello definito nella stessa maniera dai due vertici consecutivi
seguenti BC e via così
η3
, η4
... ηn,
si da la seguente DEFINIZIONE.
Si dice poligono convesso ABCDEF .. la
figura intersezione di tutti i semipiani
η1,
η2
... ηn
(La definizione di figura convessa l'avevamo già
vista nella prima dispensa)
I vertici e i lati della poligonale sono anche vertici e lati del
poligono. |
 |
|
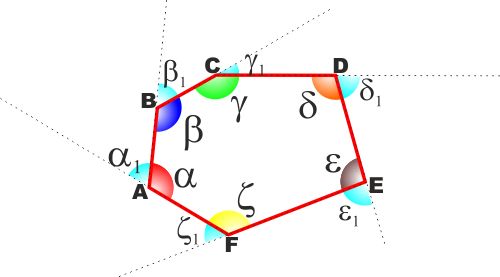 |
Osservando la figura a lato gli angoli
α β γ δ ε ζ
sono gli angoli interni del poligono,
mentre gli angoli
α1 β1 γ1 δ1 ε1 ζ1
sono gli angoli esterni.
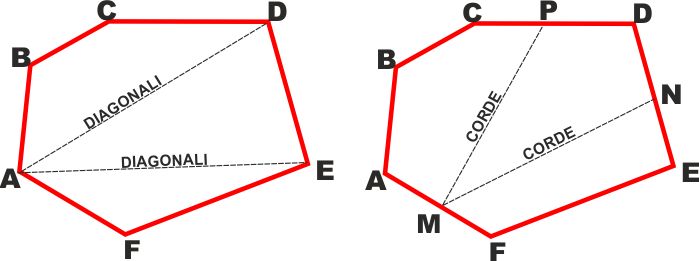
Un segmento che unisce due vertici non consecutivi si chiama
"diagonale" (ad es. AE o AD), mentre un segmento che unisce due
punti del contorno non appartenenti allo stesso lato si dicono
"corda" (ad es. MN o MP) |
|
 |
|
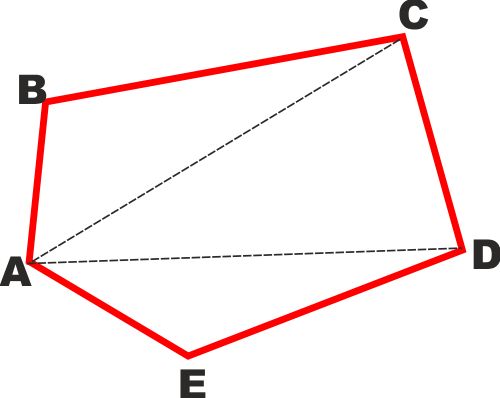
TEOREMA: In un poligono ciascun lato
è minore della somma di tutti gli altri lati.
E' analogo a quello che abbiamo già visto per i triangoli lo
dimostriamo così:
Tiriamo le diagonali per A a D e a C.
Sappiamo che ogni lato di un triangolo è minore della somma degli
altri due, quindi:
AB<BC+AC
AC<CD+AD
AD<AE+ED
Sommando membro a membro
AB+AC+AD<BC+AC+CD+AD+AE+ED
Tirando via i termini uguali (AC e AD)
AB<BC+AD+AE+ED
Come volevamo dimostrare.
|
 |
Da quanto abbiamo detto ora ne deriva che la distanza tra due punti
è il segmento che li unisce.
Ovvero la linea retta che unisce due punti A e B è SICURAMENTE più
breve della somma di tutte le spezzate che si possono percorrere per
raggiungere B da A passando per altri punti. |
|
|
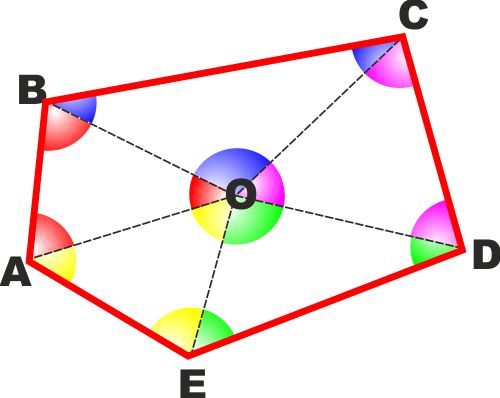 |
TEOREMA: La somma degli angoli interni
di un poligono convesso è uguale a tanti angoli piatti quanti sono i
lati che lo compongono meno un angolo giro.
Come si vede dalla figura a lato è sempre possibile scomporre un
poligono convesso in tanti triangoli quanti sono i lati, aventi
tutti un vertice in comune e a due a due adiacenti.
Come sappiamo la somma degli angoli interni di un triangolo è un
angolo piatto e di conseguenza per un poligono di n lati è n volte
un angolo piatto.
Per avere la somma degli angoli interni del poligono (che sono a due
a due la somma degli angoli interni dei triangoli in cui lo abbiamo
scomposto) basterà quindi sottrarre l'angolo giro formato dagli
angoli consecutivi al centro.
Detto π
il valore di un angolo piatto ne ricaviamo che per un poligono di
n lati la somma degli angoli interni è nπ-2π
o, se preferite
S (somma angoli interni) =
(n-2)π.
|
|
TEOREMA: La somma degli angoli esterni di
un poligono convesso è uguale a un angolo giro, indipendentemente da
quale sia il numero dei lati. Ricordo che ogni angolo
esterno è il supplementare dell'angolo interno adiacente.
Quindi la somma degli angoli interni più gli angoli esterni è
uguale a tanti angoli piatti quanti sono i vertici (e quindi i lati)
del poligono.
Se a questa somma togliamo la somma degli angoli interni otteniamo
la somma dei soli angoli esterni.
Procedendo
S1 (somma degli angoli esterni) = nπ-(nπ-2π)
cioè nπ-nπ+2π
e quindi S1= 2π
|
 |
|
SIMMETRIE |
Abbiamo già un'idea intuitiva di cosa sia una "simmetria" ne abbiamo
già viste quando abbiamo "ribaltato" una figura attorno ad un asse,
ottenendo una figura congruente seppure "speculare" rispetto
all'originale.
Diamo ora un definizione "rigorosa" di simmetria.
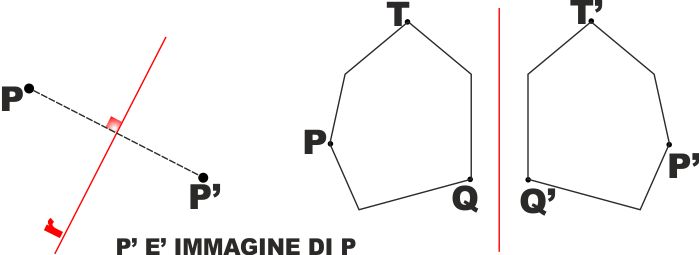
DEFINIZIONE: Due punti A e A' si
dicono simmetrici rispetto ad una retta r se la retta r è l'asse del
segmento AA'
DEFINIZIONE: Due figure si dicono
simmetriche rispetto ad una retta r se ogni punto dell'una è
simmetrico rispetto a r di ogni punto dell'altra e viceversa.
In una simmetria ad ogni punto di una figura corrisponde
uno ed un solo punto dell'altra.
Questi punti si dicono corrispondenti o omologhi o immagine l'uno
dell'altro.
|
 |
|
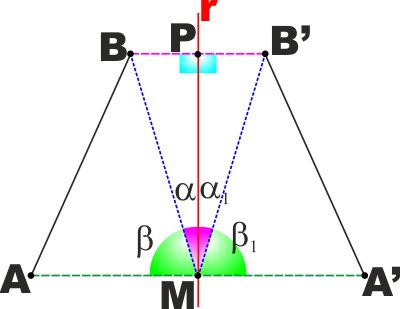 |
TEOREMA : In una simmetria assiale la
distanza tra due punti è uguale alla distanza delle rispettive
immagini.
Con riferimento alla figura a lato abbiamo per ipotesi AM=MA'
e BP=PB', che l'angolo in P è retto, così come l'angolo in M.
Vogliamo dimostrare che AB=A'B'.
Uniamo B con M B' con M - i triangoli BMP e B'MP sono uguali perché
hannoPM in comune
P retto
BP=PB' per ipotesi.
Sono quindi uguali per il 1° criterio di uguaglianza dei triangoli.
Prendiamo ora MBA e MB'A' anch'essi sono uguali perché hanno
AM=MA' per ipotesi
β=β1
in quanto complementari degli angoli uguali
α e
α1
BM=B'M perché lati corrispondenti dei triangoli uguali MBP e MB'P.
Sono quindi uguali per il !° criterio di uguaglianza dei triangoli
E quindi anche AB=A'B' , come volevamo dimostrare. |
COROLLARI:
Da quanto appena detto ne segue :
- Due figure simmetriche sono uguali
- La figura corrispondente ad una retta è una retta
- A rette parallele corrispondono rette parallele
- A due rette incidenti che formano un angolo
α
corrispondono due rette incidenti che formano un uguale angolo
α.
|
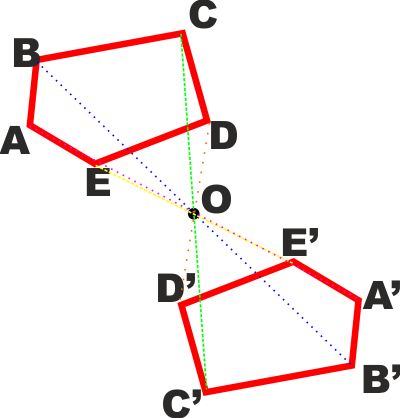 |
Definiamo ora la SIMMETRIA RISPETTO AD UN
PUNTO.
Due punti A e A' si dicono simmetrici
rispetto al punto O se il punto O è il punto medio del segmento AA'.
Due figure si dicono simmetriche rispetto ad un punto O se TUTTI i
punti corrispondenti delle due figure sono simmetrici rispetto ad O |
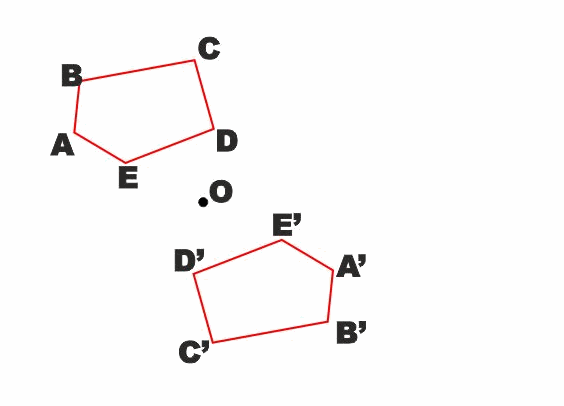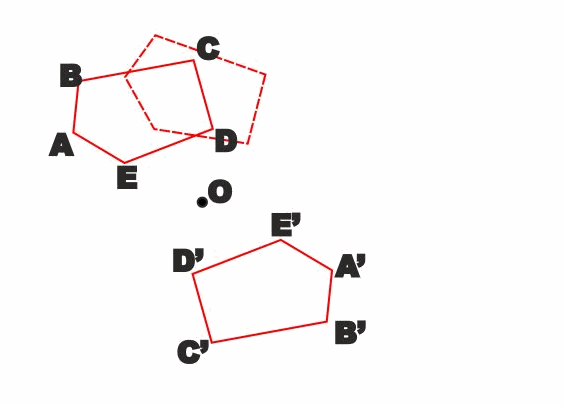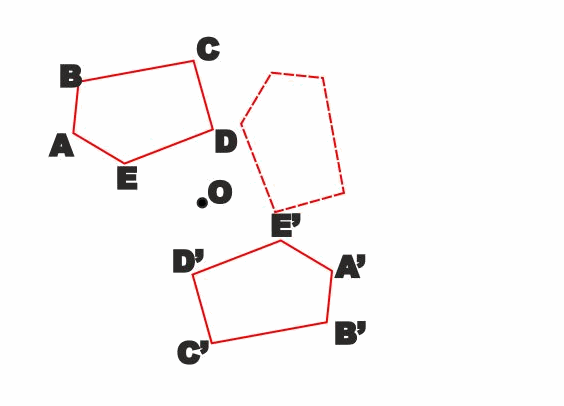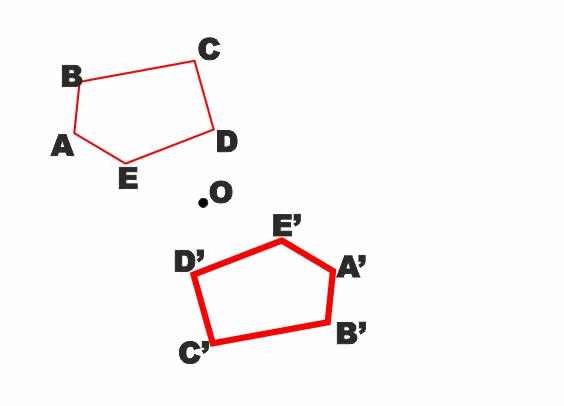
Osserviamo che in pratica due figure simmetriche rispetto ad un
punto O sono la stessa figura a cui è stata fatta fare una rotazione
piana di 180° con centro nel punto O.
Quindi oltre alle stesse proprietà che abbiamo visto per le figure
simmetriche rispetto ad una retta possiamo aggiungere che in due
figure simmetriche rispetto ad un punto due segmenti corrispondenti
risultano paralleli.
Lascio a voi dimostrare inoltre che:
- Un triangolo isoscele ha come asse di simmetria la retta su
cui giace l'altezza relativa alla base.
- Un triangolo equilatero ammette tre assi di simmetria
- Un triangolo scaleno non ammette alcun asse di simmetria
- Nessun triangolo, e in genere nessun poligono con numero
dispari di late ammette un centro di simmetria.
|
 |
|
QUADRILATERI PARTICOLARI |
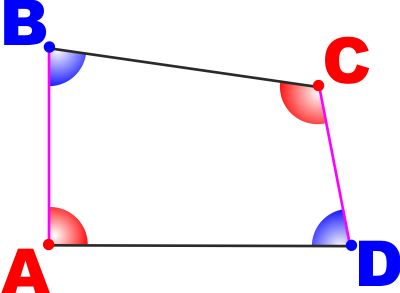
DEFINIZIONI: In un quadrilatero (poligono con 4 lati) si
dicono OPPOSTI:
- Due lati privi di vertici in comune
- Due angoli privi di lati in comune
- Due vertici non appartenenti ad uno stesso lato
|
 |
|
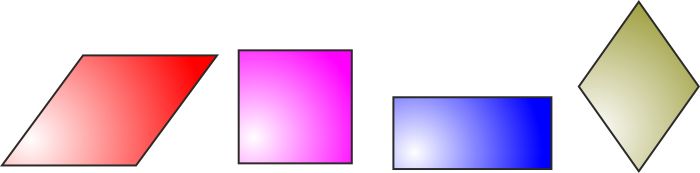 |
DEFINIZIONE: Si dice
PARALLELOGRAMMA un quadrilatero avente i lati
opposti a due a due paralleli
A lato
- Un parallelogramma qualsiasi
- Un quadrato (tutti i lati uguali e tutti gli angoli retti)
- Un rettangolo (tutti gli angoli uguali e di conseguenza
retti)
- Un rombo (tutti i lati uguali)
|
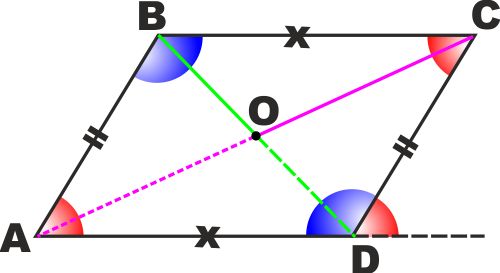
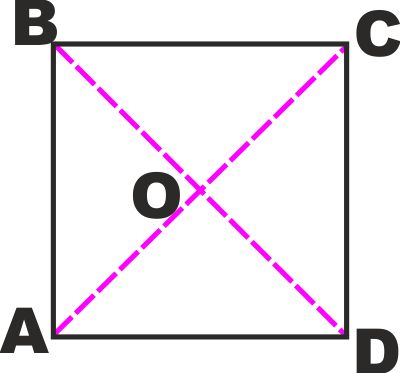
TEOREMI: In ogni parallelogramma:
- Le diagonali (sono solo due) si
intersecano in un punto.
- Le diagonali si tagliano
scambievolmente a metà.
- I due triangoli in cui esso rimane
diviso da una diagonale sono uguali
- I lati opposti sono uguali.
- Gli angoli opposti sono uguali
- Gli angoli adiacenti a ciascun lato
sono supplementari
- Ogni parallelogramma è una figura
simmetrica rispetto al punto O di intersezione delle sue
diagonali.
Lascio a voi le dimostrazioni come esercizio.
|
 |
Valgono, e anche qui lascio a voi le dimostrazioni, anche i seguenti
criteri per riconoscere se un quadrilatero è un parallelogramma:
- Un quadrilatero le cui diagonali si
tagliano scambievolmente per metà è un parallelogramma
- Un quadrilatero con i lati opposti
a due a due uguali è un parallelogramma
- Un quadrilatero con gli angoli
opposto a due a due uguali è un parallelogramma
- Un quadrilatero con due lati
opposti e paralleli è un parallelogramma
|
|
|
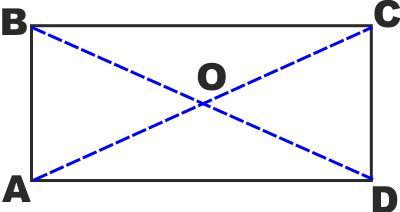
Il RETTANGOLO Si dice rettangolo un quadrilatero con tutti gli
angoli uguali
Si dimostra che:
- In un rettangolo tutti gli angoli
sono retti
- I lati opposti sono a due a due
uguali
- Le diagonali di un rettangolo sono
uguali
- Il rettangolo ammette come assi di
simmetria le due rette passanti per il centro e perpendicolari
ai lati
|
 |
|
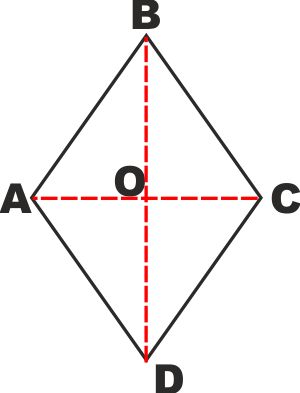
Il ROMBO Si dice rombo un quadrilatero con tutti i lati uguali
Si dimostra che:
- Le diagonali di un rombo sono
perpendicolari
- Le diagonali bisecano gli angoli
interni
- Le diagonali sono assi di simmetria
per il rombo
|
 |
|
Il QUADRATO Si dice quadrato un quadrilatero con tutti i lati
uguali e tutti gli angoli uguali
Direi "ovviamente" gode di tutte le proprietà del rettangolo e del
rombo oltre a quelle comuni a tutti i parallelogrammi. |
 |
DISTANZA DI RETTE PARALLELE
Dimostriamo il
TEOREMA: Date due distinte rette
parallele tutti i punti di ciascuna di esse hanno dall'altra la
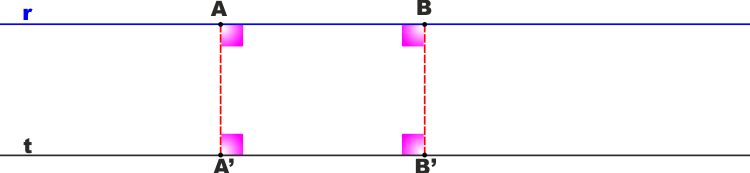
stessa distanza.Siano r e t due rette parallele,
prendiamo su r due punti A e B e siano A' e B' le proiezioni di A e
B su t.
Il quadrilatero ABB'A' è un rettangolo, avendo tutti gli angoli
retti.
Pertanto ha anche i lati opposti a due a due uguali.
Come volevamo dimostrare.
Da questo teorema discende la definizione di "distanza tra rette
parallele" che è la distanza tra un punto qualunque di una retta e
l'altra retta.
E l'affermazione che "la distanza tra due rette parallele è
costante" |
 |
|
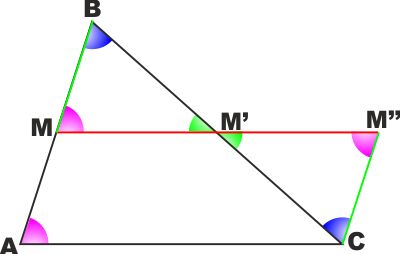 |
TEOREMA: Il segmento che unisce
i due punti medi dei lati di un triangolo (qualsiasi) è parallelo al
terzo lato e uguale alla metà di questo. Sia ABC un
triangolo qualsiasi e sia M il punto medio del segmento AB.
Portiamo da C un segmento CM'' parallelo ad AB di lunghezza pari ad
AM (e quindi anche a MB).
Uniamo M con M''.
I triangoli MM'B e CM'M'' sono uguali perché :
MB=CM'' per costruzione
L'angolo in C = angolo in B perché alterni interni della trasversale
BC che taglia le parallele CM'' e MB
L'angolo in M = angolo in M'' perché alterni interni della
trasversale MM'' che taglia le parallele CM' e MB
Sono quindi uguali per il 2° criterio di uguaglianza.
Abbiamo quindi che BM' = M'C (il segmento MM'' taglia il lato BC in
due parti uguali)
AM è parallelo e uguale a CM'' per costruzione
Quindi il quadrilatero AMM''C è un parallelogramma.
E quindi MM'' è parallelo ad AC. |
DEFINIZIONE: Si dice TRAPEZIO ogni
quadrilatero non intrecciato che abbia una coppia di lati paralleli
e gli altri due non paralleli.
- Nei trapezi i due lati paralleli vengono chiamati BASI
e si riconosce una BASE MAGGIORE e una BASE MINORE.
- I lati opposti non paralleli vengono chiamati LATI
OBLIQUI o anche semplicemente LATI
- In tutti i trapezi gli angoli adiacenti a ciascuno dei due
lati obliqui sono supplementari (coniugati interni rispetto al
lato trasversale che taglia le due basi parallele)
- Un trapezio si dice RETTANGOLO se se uno dei lati
obliqui è perpendicolare alle basi
- Un trapezio si dice ISOSCELE se i due lati obliqui
sono uguali.
TEOREMI (per i trapezi isosceli)
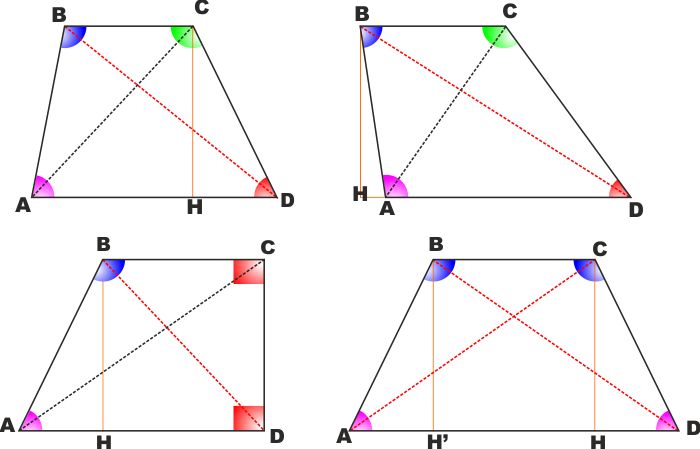
Nei trapezi isosceli (con riferimento alla figura a lato)
- Le proiezioni dei lati obliqui
sulla base maggiore sono uguali (AH' = DH)
- Gli angoli adiacenti a ciascuna
base sono uguali
- L'asse (r) di una base è asse anche
dell'altra
- Tale retta (r) è asse di simmetria
del trapezio e su di essa si incontrano le diagonali e le due
rette a cui appartengono i lati obliqui
- Le diagonali sono uguali
|
 |
|
Con riferimento alla figura : Si consideri il trapezio isoscele
ABCD su base maggiore AD.
Si portino da Ce D, estremi della base minore, le proiezioni H e H'
sulla base maggiore AD.
I triangoli rettangoli ABH' e CDH sono uguali in quanto hanno
Le ipotenuse uguali per ipotesi
Il cateto BH' = CH perché distanza tra le due rette BC e AD
parallele.
Ne consegue l'eguaglianza degli angoli A e D e B e C e delle
proiezioni AH' di AB e HD di CD.
Consideriamo i triangoli ABD e ADC
Sono uguali in quanto hanno
AD in comune
AB=CD per ipotesi
Gli angoli in D e in A uguali perché lo abbiamo appena dimostrato.
Ne consegue che la diagonale AC = BD
|
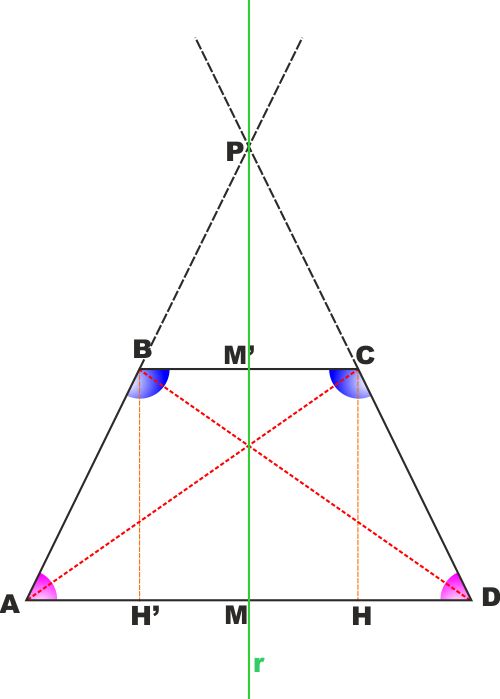 |
Tracciamo la retta r perpendicolare ad ambedue le basi e che passa
per il punto M medio della base maggiore AD e che passa per M' sulla
base minore.
é MH= MH' in quanto differenza dei segmenti uguali AM=MD per
costruzione e AH'=HD perché appena dimostrato.
Abbiamo già detto che BCHH' è un rettangolo e di conseguenza r ne è
asse di simmetria.
I trapezi MM'CB e MM'BA sono quindi uguali in quanto tutti i loro
lati e i loro angoli sono a due a due uguali.
Quindi r è asse di simmetria anche per il trapezio ABCD.
Consideriamo infine il triangolo APD dove P è il punto di
intersezione delle due rette a cui appartengono i lati obliqui AB e
CD.
APD è isoscele in quanto ha gli angoli alla base uguali.
Pertanto la mediana, l'altezza e bisettrice riferite alla base e al
vertice superiore coincidono e sono assi di simmetria e contengono
il vertice P.
Poteva bastare comunque il fatto che le AB e CD sono simmetrici
rispetto ad r e quindi lo sono anche le rette che li contengono.
Di conseguenza, come abbiamo visto, il punto di intersezione tra una
delle due e l'asse di simmetria è anche punto di intersezione con
l'asse per l'altra. |