|
Se, ad esempio, ho vento favorevole all'andata, in
un'ora percorro più strada di quanta ne percorrerò al ritorno. Se avessi
un'autonomia di due ore e mi allontanassi per un'ora, nell'ora che mi
resta non riuscirei a ripercorrere la stessa strada e a rientrare.
Questo è ancora uno dei classici problemi da impostare e risolvere
grazie all'algebra.
Limitiamoci infatti a "descrivere" in forma matematica (e cioè sotto
forma di relazioni numeriche) i dati del nostro problema.
Il mio aereo volerà per un tempo
TA di
allontanamento e per un tempo
TR di rientro. La somma dei due tempi dovrà
essere uguale proprio alla mia autonomia (normalmente indicata con
E, dall'inglese "Endurance").
Una prima relazione sarà, semplicemente
TA +
TR
= E.
E da sola ci dice poco, ma andiamo avanti...
Una volta calcolate, tenendo conto del vento, le
GSA e
GSR, velocità al
suolo di allontanamento e di rientro, potremo scrivere, ancora
semplicemente, che lo spazio percorso
AB all'andata è
uguale alla velocità di allontanamento GSA
per il tempo di allontanamento
TA.
AB =
GSA x
TA
Nello stesso modo lo spazio percorso al rientro
BA è uguale alla
velocità di rientro GSR
per il tempo di rientro
TR.
BA =
GSR
x TR
E, ancora, se ce ne fosse bisogno, che lo spazio
AB
percorso all'andata deve essere uguale a quello percorso al
rientro BA (vado e torno sullo
stesso aeroporto).
AB =
BA
L'algebra ci insegna che se abbiamo tante equazioni quante
sono le incognite il nostro "sistema lineare" è risolvibile.
E in questo caso é:
(1) TA
+ TR
= E
(2)
AB = GSA
x TA
(3)
BA =
GSR
x TR
(4) AB
= BA
abbiamo 4 incognite (TA
-
TR
- AB
- BA) e 4
relazioni. Facciamo sistema e risolviamo.
Sostituiamo la (2) e la (3) nella (4), otteniamo:
(5) GSA
x TA
= GSR
x TR
Risolviamo la (1) rispetto a
TR
:
(6) TR
= E -TA
Sostituiamo nella (5) a
TR
il suo valore espresso dalla (6) e otteniamo
un'unica relazione nell'unica incognita
TA:
GSA x
TA
= GSR
x (E -TA)
Questa è una semplice equazione che possiamo risolvere senza troppi
problemi (cioè, se abbiamo un minimo di dimestichezza con l'algebra).
I passaggi sono questi:
GSA x
TA
= GSR
x E -
GSR
xTA
GSA x
TA
+
GSR
xTA=
GSR
x E
TA
(GSA+
GSR
)= GSR
x E
E quindi, finalmente:
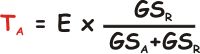
Una volta ottenuto
TA si
trova facilmente TR
(basta sostituire il valore trovato di
TA
nella (1).
Quindi, se serve, sostituendo
TAo
TR nella (2) o nella (3) si trova la distanza
AB.
A chi piace imparare le formule a memoria può memorizzare le tre
soluzioni:
Ma personalmente sconsiglio di affidare la pelle ad una
formula "imparata a memoria".
Il mio suggerimento è di imparare ad utilizzare l'algebra, impostare la
risoluzione di un qualsiasi problema semplicemente cercando di
"descriverlo" in formule matematiche.
Dopodiché non avremo più problemi: sarà l'algebra stessa, facendo solo
dei semplici conti, che ci porterà alla soluzione. |