|
Quando dobbiamo percorrere lunghe distanze, ad alta quota, distanti dalle
asperità del terreno che possono influenzare il movimento dell'aria, l'unico
tipo di vento che ci interessa è quello "geostrofico", cioè il vento
prodotto dalla differenza di pressione tra due diverse zone dell'atmosfera.
Come è logico aspettarsi, l'aria da una zona di alta pressione tende a
spostarsi verso una zona di bassa pressione, esattamente come l'aria
contenuta in una bombola (alta pressione) quando ne apriamo la valvola esce
(all'esterno la pressione è più bassa).
Un po' meno intuitivo è il motivo per cui l'aria non si muove in linea retta
ma in pratica "gira intorno" alle depressioni.
Questo è dovuto alla rotazione terrestre e ad un ben noto effetto che essa
provoca che passa sotto il nome di "forza di Coriolis". |
 |
La forza di
Coriolis |
La "forza di Coriolis", in realtà non esiste!
Cioè non è affatto una "forza".
E' semplicemente un effetto della rotazione terrestre sul moto di
"oggetti" (e non solo le grandi masse d'aria che consideriamo in
meteorologia, ma tutto quanto si muove sulla Terra) che si spostano
in direzione Sud-Nord.
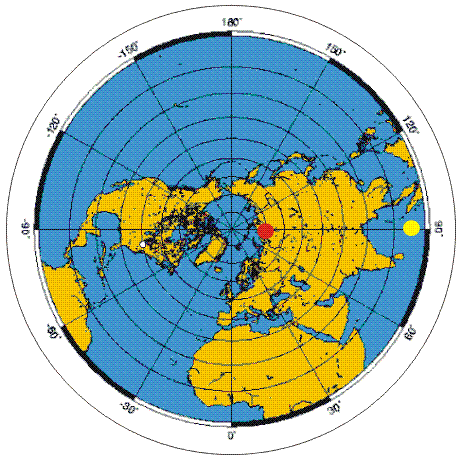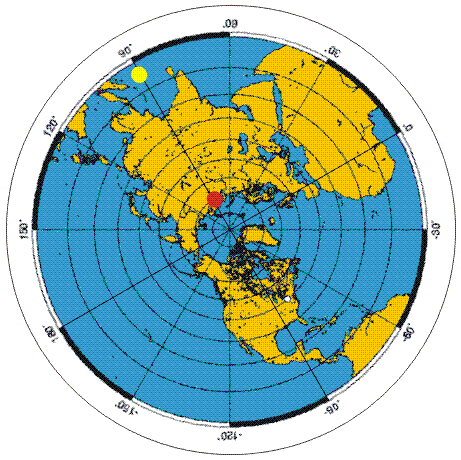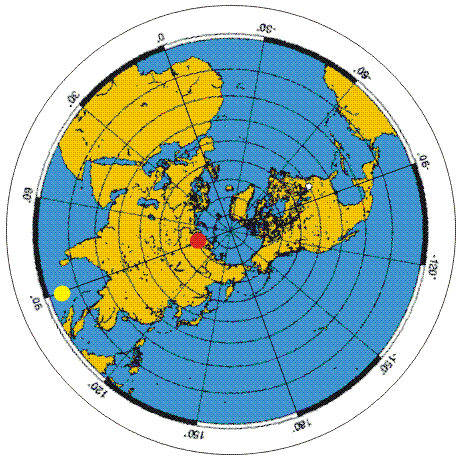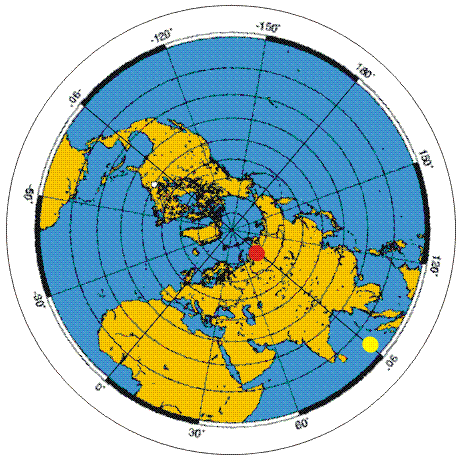
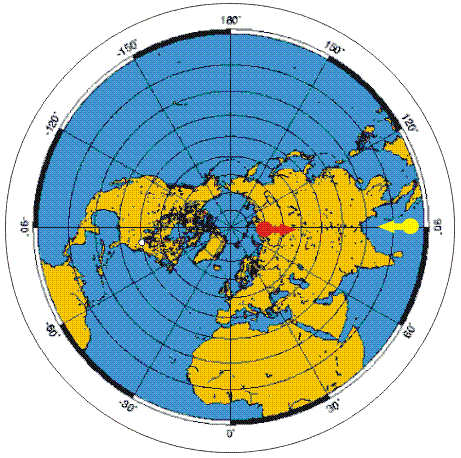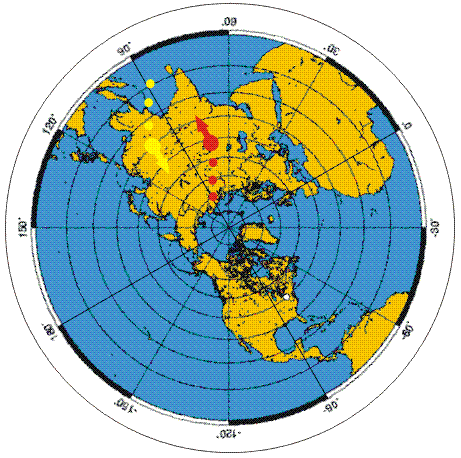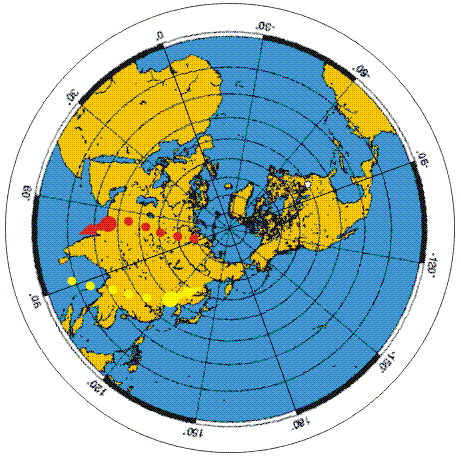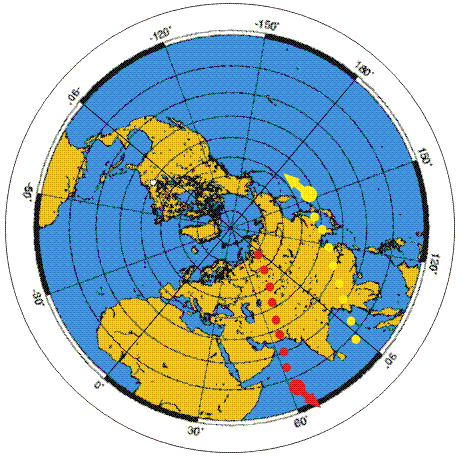
Osserviamo la figura a lato:
Il pallino rosso e il pallino giallo, visti da Terra, sono fermi,
solidali con il terreno.
Ma visti dallo spazio esterno, invece, ruotano con la stessa
velocità di rotazione della Terra.
E' evidente quindi come la velocità del pallino giallo, più lontano
dall'asse di rotazione (il Polo) sia molto più elevata di quella del
pallino rosso.
Se ora il pallino giallo si muove verso Nord (verso
il centro di rotazione), attirato ad esempio da una zona di bassa
pressione, oltre al movimento radiale (in direzione Sud-Nord)
mantiene però una velocità tangenziale (cioè diretta nello stesso
senso della rotazione) maggiore rispetto alle zone a latitudine più
elevata. |
|
Questo perché, come abbiamo visto prima, provenendo da latitudini
minori (più vicino all'Equatore, più lontano dal centro di
rotazione) possedeva già una velocità tangenziale maggiore.
Allo stesso modo il pallino rosso che si sposta verso Sud si trova
ad attraversare zone che ruotano più velocemente di lui.
In questo modo si troverà "in ritardo" rispetto al terreno.
In pratica, sia il pallino giallo che quello rosso sembrano deviare
verso destra rispetto al semplice movimento radiale Nord-Sud. |
 |
 |
 |
|
Ovviamente nell'emisfero australe il fenomeno si
verifica ugualmente ma in senso opposto.
Nelle immagini si vedono infatti il ciclone "Fabian" nella Guadalupe
(Nord - senso di rotazione antiorario) e Ingrid, in Oceania (Sud -
senso di rotazione orario). |
 |
L'accelerazione di Coriolis a cui è soggetto un
mobile che si sposti con velocità V alla latitudine
φ è:
D = W 2ω sen
φ
Dove:
- V è la velocità del mobile
- ω è la velocità angolare
di rotazione terrestre (360° in 24h ovvero 15°/h o 7.29*10-5
rad/sec)
- φ è la latitudine
|
|
|
|
 |
|
|
Rotta
"brachistocrona" |
 |
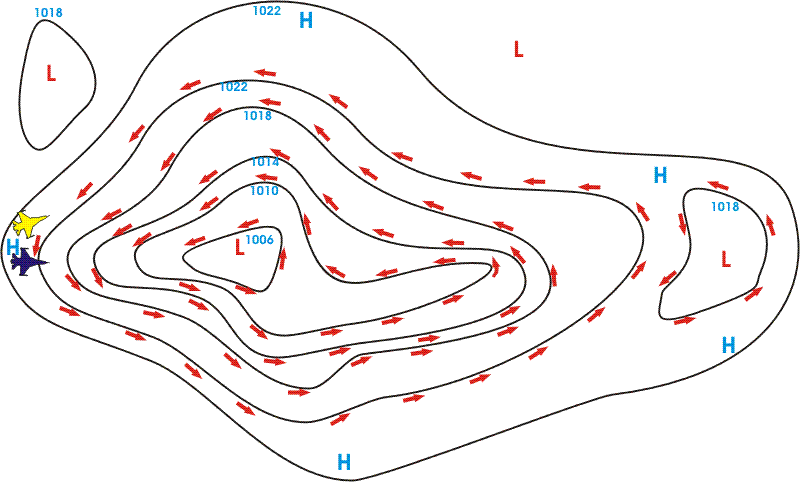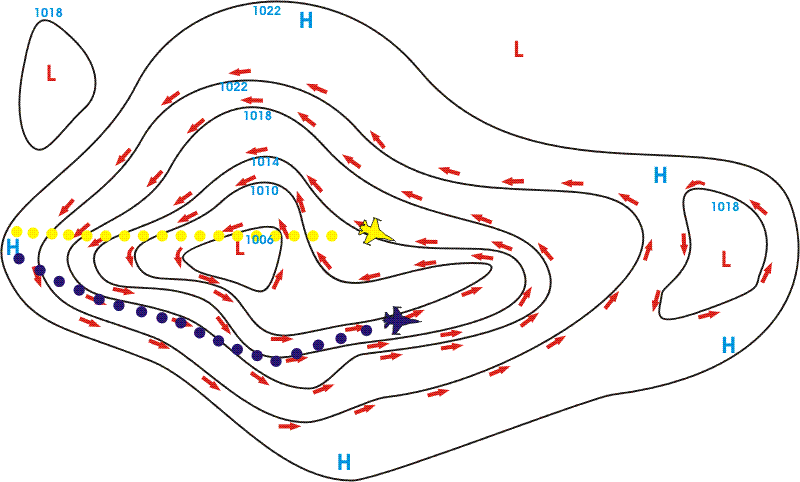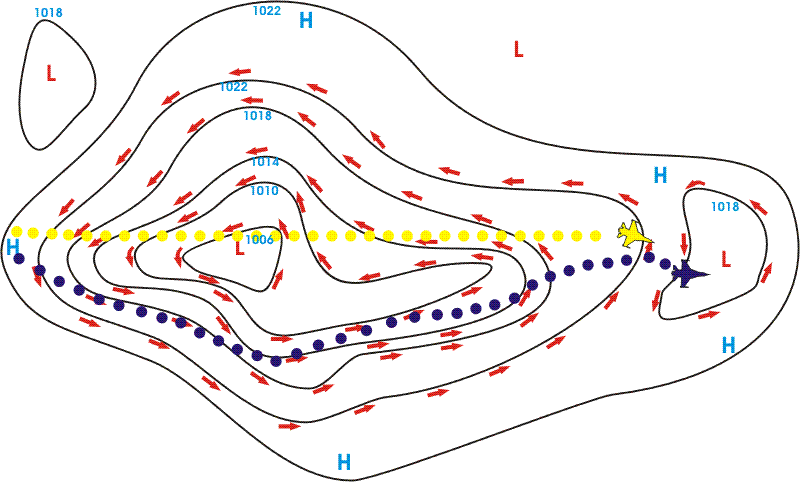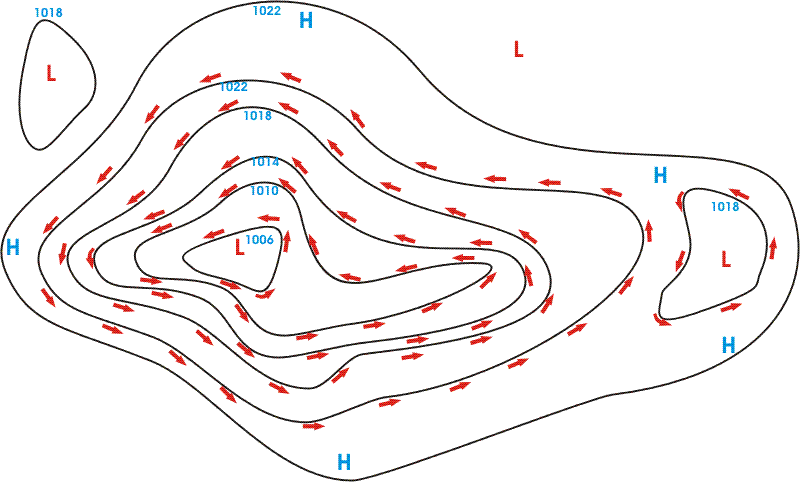
Attraversando zone delimitate da
diverse isobare, il vento cambia continuamente.
Se attraversiamo un nucleo di bassa pressione da Ovest verso Est
nell'emisfero settentrionale, il vento che incontreremo, ruotando in
senso antiorario intorno alla depressione, sarà prima diretto verso Sud
e dopo verso Nord. |
 |
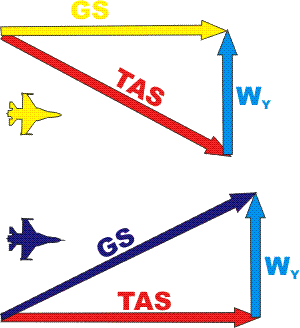
Se noi contrastassimo il vento prima
deviando verso Nord e poi verso Sud manterremmo una rotta ben definita,
rettilinea e costante, ma ci vedremmo rallentati dalla necessità di
"spendere" un po' della nostra TAS per contrastare appunto la deriva prodotta dal vento. |
| |
 |
Se invece ci lasciamo trasportare dal vento
senza preoccuparci della deriva, questo prima ci sposterà verso Sud e
poi a Nord, ma alla fine, pur avendo percorso più strada, saremo stati
più veloci. |
Questo perché avremo mantenuto
nella direzione della nostra rotta ideale una componente di velocità
sempre uguale a tutta la nostra TAS, che in questo modo non "consumiamo"
per contrastare la deriva.
La rotta seguita dal velivolo blu, più lunga ma più veloce, si dice
"brachistocrona". |
Per arrivare correttamente a
destinazione senza disperdere energie (e carburante), ci converrà
quindi, invece di contrastare il vento su ogni tratto, limitarci a
contrastare la deriva del solo "vento medio", che possiamo vedere come
un vento costante lungo tutto la rotta che equivalga alla sommatoria
pesata del vento reale che incontreremo istante per istante.
Somma vettoriale, ovviamente, per cui il vento diretto verso Sud si
annulla con l'equivalente diretto verso Nord.
Siccome, come già visto, il vento è geostrofico, quindi prodotto solo
dalle differenze di pressione e parallelo alle isobare, si dimostra che
il vento "medio" su una determinata rotta dipende solo dal valore delle
isobare iniziale e finale, dalla lunghezza del tragitto stesso e, come
al solito, visto che parliamo di effetti della rotazione terrestre,
dalla latitudine φm media
alla quale voliamo, ed è indipendente dai valori delle isobare che
incontriamo durante il tragitto,. |
|
|
Calcolo del vento
medio in rotta |
L'aria si sposta a causa della differenza di pressione
tra due zone dell'atmosfera.
Su una lunghezza L avremo :
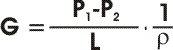
Dove P1 e P2 sono le due
pressioni, L è la distanza tra le isobare e
ρ, come sempre, la densità dell'aria.
A "regime", cioè quando il vento diviene costante le due accelerazioni G
(di gradiente) e D (deviazione di Coriolis) devono equilibrarsi, deve
cioè essere:
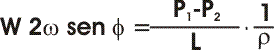
da cui si ricava facilmente la velocità del vento W:
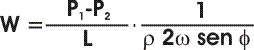
Per motivi pratici, però, le carte in quota non riportano delle
isobare ma delle "isoipse", che sono curve che definiscono i punti dove
un dato valore di pressione si trova alla medesima quota.
Questo perché è più facile e diretto andare a vedere a che quota mi
ritrovo una certa pressione che non viceversa che pressione trovo ad una
certa quota.
Questo discorso un po' macchinoso in realtà ha una spiegazione piuttosto
semplice: gli altimetri dei velivoli sono in pratica dei barometri e,
come abbiamo già visto, quando si vola in quota si mantengono "livelli
di volo" e cioè bene definite quote di pressione.
Un velivolo che vola a FL 100 non vola a 10.000 piedi di quota, ma
sull'isobara che "dista 10.000 piedi" dalla isobara standard di 1013 mb.
Con il radar altimetro sarà poi semplice individuare a che quota si è.
Considerando che P1 = P2 +
g Δh , dove g è l'accelerazione di
gravità e Δh la colonna d'aria tra le
due isobare, cioè la differenza di quota tra le due isoipse, la formula
si riscrive così:
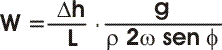
Dove L stavolta è la distanza tra le isoipse. |
|
Calcoliamo ora la sola componente del vento al
traverso, che è quella che ci serve per impostare un'eventuale
correzione della deriva.
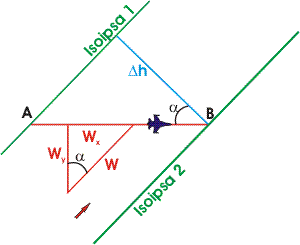
Dall'esempio riportato a lato si vede come tra il vento e la sua
componente normale alla rotta Wy e tra il tratto
percorso AB e la distanza tra le isoipse
Δh vi sia lo stesso rapporto (in
quanto i due triangoli sono simili).
In questo modo è facile ricavare la formula che diventa:
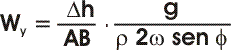
Da cui si vede come la deriva dipenda in pratica
solo dai valori iniziale e finale delle pressioni (le due isoipse),
dalla latitudine e dalla distanza AB. |
|
|
|
|
|
|
|