|
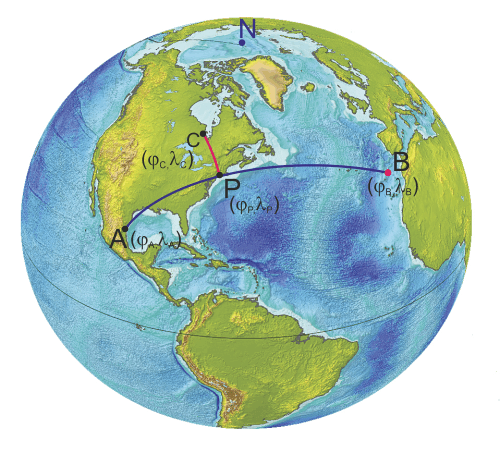
Vediamo come trovare la distanza di un punto da una rotta ortodromica.
Supponiamo di voler conoscere
quanto dista il punto C da una determinata ortodromia tra i punti
A e
B, e di voler conoscere le coordinate del punto
P, che si trova su questa rotta ed è il punto più vicino al punto
C.
 |
Per prima cosa risolviamo l'ortodromia tra A e
B, individuando
come abbiamo imparato a fare la distanza
c e almeno uno dei due angoli a o b - tanto per cambiare oggi lavoriamo su b- .
La distanza d del punto
C dall'ortodromia è un'altra ortodromia (ovviamente) che passa per
C e che forma con l'ortodromia AB un angolo di 90° - come sarebbe nel piano per la distanza di un punto da una retta o da una curva.
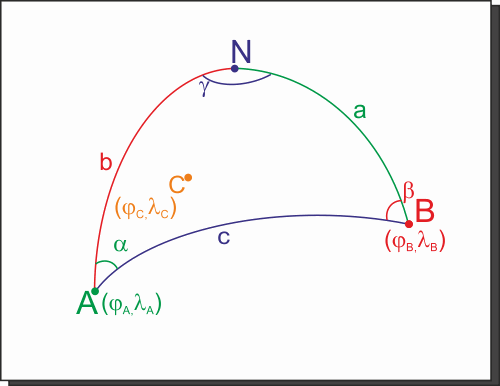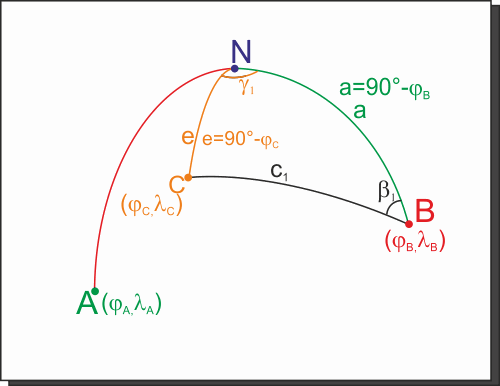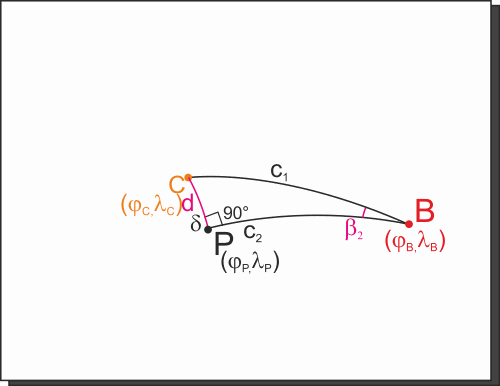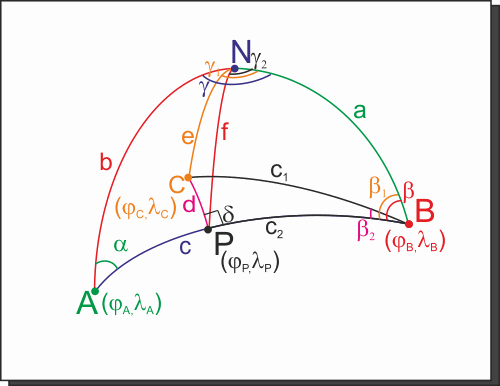
Poi calcoliamoci l'ortodromia
BC, trovando la distanza
c1 e l'angolo
b1.
A questo punto possiamo calcolareb2 come differenza tra b e
b1.
|
|
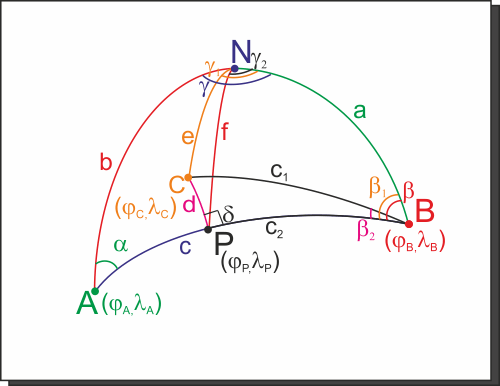
Applicando il teorema dei seni, conoscendo
c1 e l'angolo opposto
d di 90° e conoscendob2 che abbiamo appena calcolato come differenza tra b eb1, possiamo trovare il lato
d, distanza tra
C e l'ortodromia.

|
|
A questo punto restano da calcolare
le coordinate del punto P.
Siccome il triangolo
BPC è retto in
P, possiamo usare la formula di Eulero semplificata come già abbiamo visto quando abbiamo imparato a
trovare il vertice.
In questo modo calcoliamo c2, distanza tra
B e
P.
 |
Per valutare f, distanza tra
P e il Polo Nord, applicherò ancora la formula di Eulero, questa volta al triangolo
ABN, di cui conosco i lati
a e
c2 e l'angolo tra essi compreso
b.

Trovato f applico di nuovo il teorema dei seni per trovare g2

e finalmente trovo le coordinate di P.

Ricordando che il valore della longitudine deve esser valutato tenendo conto del fatto che
B si trovi ad Est o ad Ovest di Greenwich e che il valore di g2
sia eventualmente pił o meno grande della longitudine di
B |