Il problema dell'intercettazione consiste
nell'individuare la prua da mantenere per "intercettare" un altro
velivolo (o qualsiasi "mobile") di cui siano note traiettoria e
velocità.
Prima di tutto vediamo di individuare quale è la condizione necessaria
affinché due velivoli siano in "rotta di collisione".
Indipendentemente dalle considerazioni che faremo in seguito,
verifichiamo che già a livello inconscio e istintivo noi siamo
perfettamente in grado di capire quale è la condizione che dobbiamo
mantenere per intercettare un altro mobile.
Pensiamo a quando un passante ci attraversa la strada davanti, mentre
guidiamo il motorino...
L'unico senso coinvolto è la vista, e senza fare alcun calcolo sappiamo
al volo se il passante passerà prima di noi, se gli passeremo davanti, o
se invece dobbiamo rallentare perché gli stiamo andando addosso. |
 |
 |
 |
Osservando le tre figure qua sopra è
evidente che nel primo caso l'F16 ci sfilerà davanti, nel secondo siamo
in rotta di collisione, nel terzo, infine, saremo noi a sfilare di prua
al caccia.
Cosa cambia, nel nostro campo visivo, che ci fa capire il moto relativo
tra il nostro velivolo e l'F16?
Nel primo caso, quando l'F16 ci sfila di prua, la sua posizione nel
nostro campo visivo cambia, passando da destra a sinistra.
Nel terzo, nuovamente la sua posizione cambia e lo vediamo sfilarci da
sinistra a destra.
Nel secondo caso, invece, l'F16 rimane sullo stesso rilevamento (nella
stessa posizione rispetto al nostro campo visivo).
Senza calcoli abbiamo evidenziato subito come già inconsciamente
possedevamo la soluzione del nostro problema:
perché due mobili siano in rotta di collisione
è necessario e sufficiente che mantengano costante il rilevamento
reciproco. |
| Diamone ora una dimostrazione più
rigorosa: |
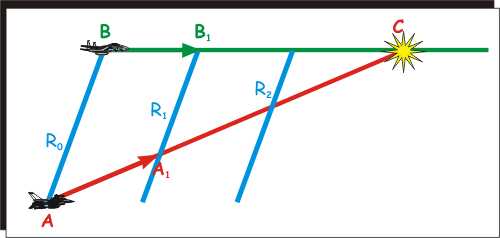 |
Nella figura seguente si vede come affinché
C sia il punto di
intercettazione, occorre che
B percorra la
distanza B-C
nello stesso tempo in cui
A percorre A-C.
Se i segmenti B-B1
e A-A1
rappresentano le velocità di
B e di
A, e si mantiene
costante il rilevamento R0,
R1,
R2...
tutti i triangoli ABC,
A1B1C,
... sono simili tra loro, e cioè tutte le coppie
A-C/B-C,
A1-C/B1-C...
sono tra loro direttamente proporzionali. |
| Ma se i segmenti
B-B1 e
A-A1
rappresentano le velocità dei due velivoli, è proprio, per definizione,
il tempo T1 che
A impiega per
percorrere A-A1
lo stesso tempo T1 in cui
B percorre
B-B1, e
siccome tutti i segmenti
B-B1,
B-B2,
...., B-C sono
proporzionali ai rispettivi
A-A1,
A-A2,
...., A-C,
in quanto segmenti individuati su due rette dal fascio di rette
parallele R0,1,...,n,
anche il tempo T che
A impiega a
percorrere l'intero percorso
A-C
è uguale al tempo in cui B
percorre B-C.
|
|
Risoluzione grafica |
Vediamo adesso l'algoritmo grafico.
Il problema è, dati traiettoria e velocità dell'intercettato, il vento e
la TAS dell'intercettore, trovare la giusta prua da mantenere per
eseguire l'intercettazione.
Ovviamente dovremo tener conto anche del vento, e la nostra velocità
sarà come sempre la risultante tra il vento e la TAS.
Dovremo quindi costruire un triangolo del vento con la condizione di
mantenere inalterato il rilevamento iniziale. |
|

|
Tracciato il rilevamento iniziale
R0 e la
velocità di B,
riportiamo su questa una retta
R1
parallela al rilevamento iniziale
R0.
Costruiamo quindi il nostro triangolo del vento costringendo la punta
del vettore TAS a finire
proprio sul nuovo rilevamento
R1.
La nostra GSA,
risultante di vento e TAS, sarà
quella da mantenere per intercettare
B, e prolungandola
incontriamo la traiettoria di
B nel punto
C, di
intercettazione.
Il tempo necessario all'intercettazione lo ricaveremo dividendo la
distanza B-C
per la velocità (nota) di
B.
Questo è preferibile, rispetto a misurare
A-C
e dividere per la nostra
GSA, in quanto dei valori utilizzati sia
A-C
che GSA
sono stati ricavati graficamente (e quindi ambedue affetti da errore di
misura) mentre nel primo caso solo
B-C viene ricavato
dalla figura (e quindi è affetto da errore) mentre la velocità di
B è uno dei dati
iniziali del problema (e quindi non è affetto da errore). |
|