|
Durante un volo tra un aeroporto e un'altro, uno dei problemi che si può
porre, ad esempio a causa di una sopraggiunta emergenza, è classicamente "Ci
vuol meno tempo ad arrivare a destinazione o a tornare indietro?"
Se non ci fosse di mezzo il vento la soluzione sarebbe piuttosto semplice:
se non sono ancora arrivato a metà strada faccio prima a tornare indietro,
se ho già superato la metà sarà più rapido proseguire sino a destinazione.
Ma se c'è il vento tutto cambia.
Se in una direzione ho il vento in faccia, virando di 180° me lo ritrovo in
coda.
Se prima mi rallentava adesso mi favorisce e viceversa.
Questo vuol dire che, genericamente, le velocità di andata e di ritorno
possono essere diverse.
E in questo caso il punto dal quale impiegherei lo stesso tempo a concludere
la tratta o a rientrare alla base non è più a metà del percorso.
Come risolvere?
Utilizziamo l'algebra.
Cerchiamo di descrivere il nostro problema in termini algebrici, scrivendo
le semplici relazioni che conosciamo senza preoccuparci di ragionare sulla
soluzione vera e propria e senza preoccuparci di verificare se in queste
relazioni sono presenti termini noti o incognite
Se le relazioni che scriviamo sono vere e se alla fine ci troveremo tante
relazioni (linearmente indipendenti ci dice la matematica, cioè non possiamo
scrivere due volte la stessa) quante sono le incognite, basterà risolvere
con le solite regole dell'algebra il "sistema" e la soluzione salterà fuori
senza alcuno sforzo. |
|

|
|
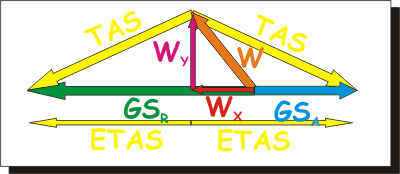
Come prima cosa calcoliamo le velocità di andata
GSA e di rientro GSR
con uno dei metodi visti per la soluzione del "triangolo del vento".
Sarà semplice, visto che le due GS
sono la somma di una ETAS sempre
uguale più una WX del
vento che una volta ci favorisce e una volta ci ostacola (una volta si somma
e una si sottrae). |
|
Conosciute le due velocità al suolo,
cominciamo a "descrivere" il problema:
A noi serve trovare il punto P tale che il tempo impiegato per rientrare
da P ad A sia uguale al tempo impiegato per completare la tratta da P a
B.
Cioè TPA
= TPB,
così, semplicemente.
Esistono poi semplici relazioni che legano i tempi alle distanze e alle
velocità, scriviamole:
Il tempo che impiego a rientrare è uguale al rapporto tra la distanza da
ripercorrere PA
e la velocità di rientro GSR.
Il tempo che ci vuole a chiudere la tratta è il rapporto tra la distanza
che rimane per arrivare PB
e la velocità di andata GSA. |
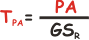 |
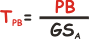 |
E poi la relazione che descrive lo spazio
nel quale ci muoviamo: semplicemente che la somma tra le distanze
PA e
PB è la nostra
tratta AB:
PA +
PB =
AB
Ci ritroviamo con quattro incognite e quattro relazioni, l'algebra ci
dice che semplicemente "mettendole a sistema" troveremo una soluzione.
(1) TPA
= TPB
(2)
PB =
TPBxGSA
(3) PA =
TPAxGSR
(4) PA
+ PB =
AB
La prima operazione che possiamo fare è sostituire le (2) e
(3) nella (4), trovando:
(5) TPAxGSR+TPBxGSA =
AB
Quindi, ricordando la (1), possiamo raccogliere ,
TPA
(o
TPB,
visto che sono la stessa cosa):
(6) TPA(GSR+GSA)=
AB
e quindi, banalmente:
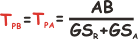
Dalle relazioni iniziali (2) e (3) possiamo ora ricavare tutte le formule risolutive,
giusto per coloro cui piace ricordarle a memoria... |
|
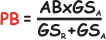
|
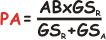
|
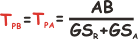
|
|