|
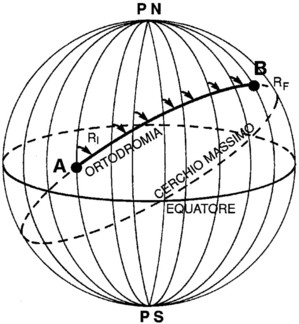
Le rotte ORTODROMICHE sono rotte che si
sviluppano lungo un arco di cerchio massimo, sulla superficie
terrestre.
Se vogliamo percorrere la via più breve tra due punti situati su
una superficie curva quale è la sfera terrestre, noi seguiremo
un percorso che, naturalmente, si sviluppa lungo un "cerchio
massimo", cioè un cerchio ottenuto sezionando la sfera con un
piano che ne contiene il centro.

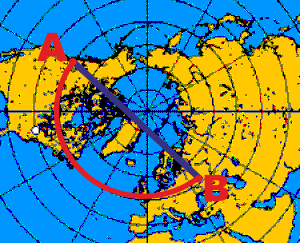
Invito a fare questo esperimento: prendete un mappamondo e un
pezzo di spago. Tirate lo spago tra due punti, sullo stesso
emisfero, a latitudini abbastanza elevate (ad esempio tra Nord
Europa e Nord America).
 |
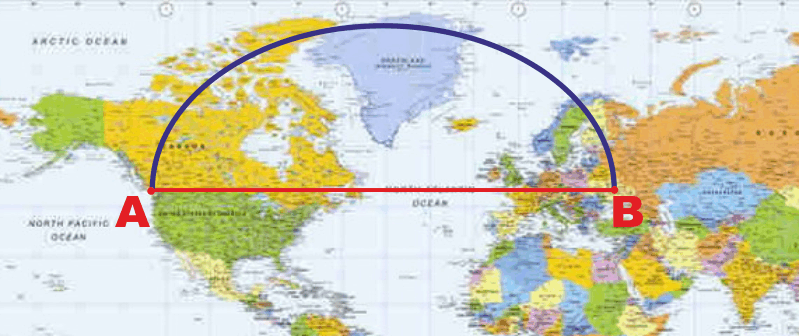
Osservate la linea su cui si dispone lo spago (lo stiamo
tirando quindi questa linea è la più breve possibile tra i
due punti): è una linea che NON mantiene lo stesso angolo di
incidenza con i meridiani e, noterete, si sviluppa "salendo"
dal primo punto verso il polo e poi ridiscendendo sino al
secondo punto.
Se rappresentassimo tale linea su una proiezione di
Mercatore, che è ottenuta proiettando la sfera su un
cilindro, e ha come caratteristica di rendere i meridiani
paralleli tra di loro, questa diventerebbe una curva. Mentre
la linea retta che tracceremmo sulla stessa cartina, se
volessimo farla seguire al nostro spago sul mappamondo, si
rivelerebbe ben più lunga.
Dalle due rappresentazioni è evidente com |
|
Per prima cosa risolviamo l'ortodromia tra A e B, individuando come abbiamo imparato a fare la distanza c e almeno uno dei due angoli a o b - tanto per cambiare oggi lavoriamo su b- .
La distanza d del punto C dall'ortodromia è un'altra ortodromia (ovviamente) che passa per C e che forma con l'ortodromia AB un angolo di 90° - come sarebbe nel piano per la distanza di un punto da una retta o da una curva.
Poi calcoliamoci l'ortodromia BC, trovando la distanza c1 e l'angolob1.
A questo bunto possiamo calcolareb2 come differenza tra b e b1.
|
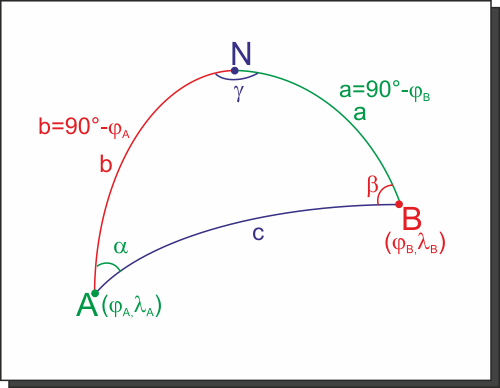 |
Applicando il teorema dei seni, conoscendo c1 e l'angolo opposto d di 90° e conoscendob2 che abbiamo appena calcolato come differenza tra b eb1, possiamo trovare il lato d, distanza tra C e l'ortodromia.
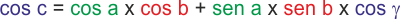

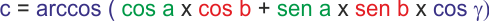
|
|
A questo punto restano da calcolare
le coordinate del punto P.
Siccome il triangolo BPC è retto in P, possiamo usare la formula di Eulero semplificata come già abbiamo visto quando abbiamo imparato a trovare il vertice.
In questo modo calcoliamo c2, distanza tra B e P.
|
Per valutare f, distanza tra P e il Polo Nord, applicherò ancora la formula di Eulero, questa volta al triangolo ABN, di cui conosco i lati a e c2 e l'amgolo tra essi compreso b.
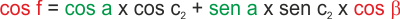
Trovato f applico di nuovo il teorema dei seni per trovare g2

e finalmente trovo le coordinate di P.

Ricordando che il valore della longitudine deve esser valutato tenendo conto del fatto che B si trovi ad Est o ad Ovest di Greenwich e che il valore di g2 sia eventualmente più o meno grande della longitudine di B |