Navigazione - dispense
Intercettazione - soluzione analitica

1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18

Vediamo ora come è possibile risolvere il problema dell'intercettazione in modo analitico.
Per metodo "analitico" intendo facendo calcoli e non prendendo misure sulla carta (modo "grafico").
Partiamo dal presupposto di avere una buona familiarità con il calcolo vettoriale.
Almeno di saper sommare vettori (significa risolvere un triangolo di cui siano noti due lati e l'angolo tra essi compreso... teorema di Carnot).
In questo caso possiamo considerare il velivolo da intercettare come se fosse fermo, e un vento di direzione opposta al suo moto, e di intensità uguale alla sua velocità, ci investisse.
Noi dovremo "risalire" questo vento esattamente come dovremmo "seguirlo".
In questo modo l'intercettazione si ridurrà ad un triangolo del vento dove la rotta da seguire sarà semplicemente il rilevamento iniziale, e il vento sarà la somma vettoriale tra il vento reale e quello fittizio che ha per direzione la stessa del velivolo da intercettare, ma verso opposto, e per intensità (o modulo) la velocità del velivolo da intercettare.
 

 Nella rappresentazione a sinistra vediamo la manovra come si svolge nella realtà.
Possiamo chiaramente distinguere come il caccia mantenga una rotta inclinata rispetto al rilevamento iniziale che gli permette, oltre che di "inseguire" l'awac, di risalire il vento.
 
Nella figura a destra vediamo la stessa situazione ma relativamente ad un sistema solidale con l'intercettato.
In questo caso il caccia sembra risalire direttamente verso l'awac, mentre deve contrastare un vento apparente somma del vento reale e dello spostamento dell'intercettato.

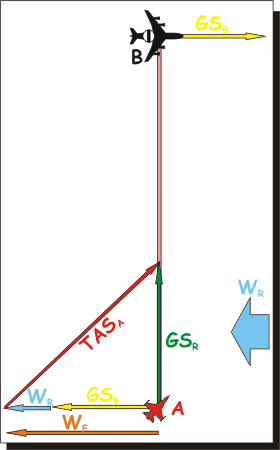In pratica si risolve un triangolo del vento dove al posto del vento reale si considera un vento fittizio WF somma del vento reale e della GSB (presa con verso opposto) dell'intercettato.
Nel caso più generale dove i due vettori non sono allineati, la somma si esegue non aritmeticamente ma geometricamente, utilizzando o un algoritmo grafico (si disegnano con precisione i vettori e si misura la risultante) o il teorema di Carnot, di cui ricordo l'enunciato:
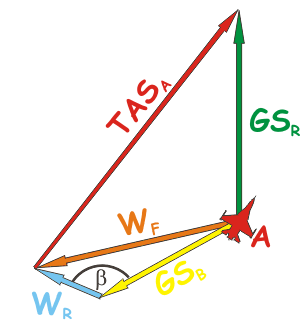In un triangolo qualsiasi di cui siano conosciuti due lati WR e GSB e l'angolo tra essi compreso β è:
WF2 = WR2 + GSB2 - 2WRGSB cos β
Una volta trovato il vento fittizio e risolto il triangolo del vento, la velocità GS trovata è la nostra velocità non più riferita al suolo, ma relativa al velivolo da intercettare.
Il tempo T necessario all'intercettazione sarà il rapporto tra la distanza iniziale AB e questa GS.
Per sapere dove è il punto P di intercettazione basterà poi valutare la posizione dell'intercettato dopo il tempo T rispetto allo stato iniziale.
Lo spazio percorso da B sarà:
BP = T x GSB.
1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18