|
Nella dispensa precedente abbiamo visto come sia
possibile valutare le forze in gioco riferite ad un sistema
statico.
Negli esempi fatti abbiamo considerato i corpi come
"puntiformi", cioè senza una forma reale.
In questo caso per garantire l'equilibrio del sistema basta che
sia nulla la risultante di tutte le forze cha agiscono su di
esso.
Ma questo in genere non basta.
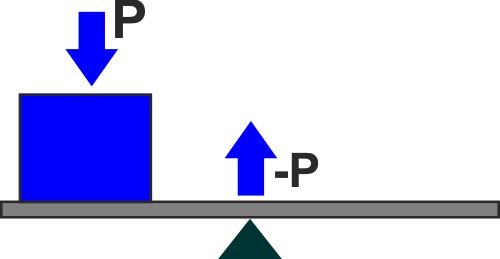
Prendiamo ad esempio un peso posizionato su una trave, a sua
volta appoggiata su un supporto, come nella figura a lato.
E' immediatamente evidente che c'è qualcosa che non va ...
Le forze sono equilibrate, ma il sistema non se ne sta fermo.
Un sistema come quello della figura qui sotto invece sarebbe
stabile. |
 |
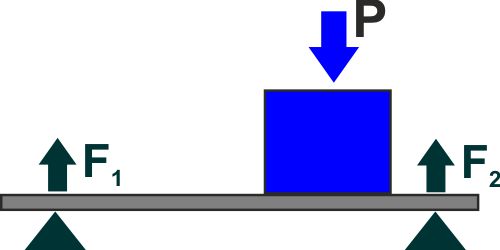 |
Ovviamente dovrà essere F1 + F2 = P
, ma sarebbe anche l'unica relazione che potremmo scrivere, e
quindi, con quello che sappiamo, non saremmo in grado di
calcolare i valori di F1 ed F2
(una sola relazione con due incognite).
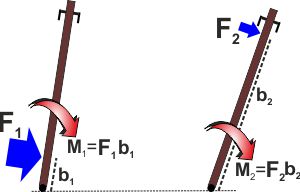
Dobbiamo definire un'altra grandezza che chiameremo MOMENTO
DI UNA FORZA e che è uguale al prodotto della forza per il
braccio di applicazione.
Cosa vuol dire?
Supponiamo di voler far ruotare una porta intorno al suo
cardine.
E' esperienza comune che se spingo la porta vicinissimo al
cardine per smuoverla devo fare una fatica enorme .. se invece
la spingo nella zona della maniglia (che non a caso è messa ben
lontana dal cardine) lo sforzo è minimo.
In pratica osserviamo che, per quanto riguarda la capacità di
far ruotare un corpo:
- Se applichiamo una forza lontana dal centro di rotazione
serve poca forza.
- Se applichiamo la forza vicino al centro di rotazione
occorre molta forza
- Se applichiamo la forza proprio sull'asse di rotazione,
per quanta forza si possa fare il corpo non ruota
|
 |
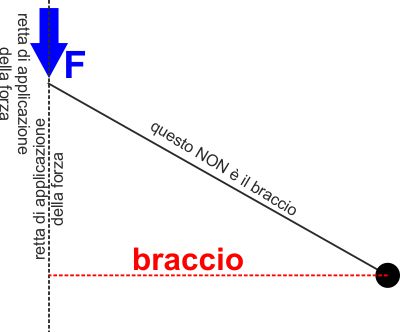
Per essere più precisi, definiamo il braccio di
applicazione:
E' la distanza tra la retta di azione della forza e il centro di
rotazione.
Prima conseguenza di questa osservazione è tutta la teoria sulle
leve.
Quanta forza devo fare per sollevare un peso di 100 kg
utilizzando un'asse di 2 metri appoggiata a 50 cm dall'estremità
su cui è fissato il peso? |
 |
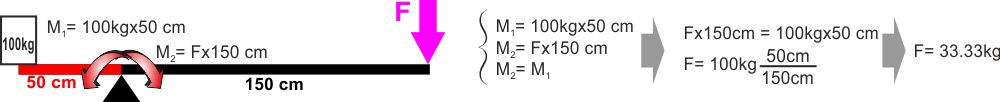 |
Questa che abbiamo visto è una delle prime macchine mai
utilizzate dall'uomo, la LEVA.
In particolare il tipo di leva mostrato qui è una LEVA DI
PRIMO GENERE - il punto d'appoggio si chiama FULCRO)
è posto tra la forza attiva e quella resistente (il peso).
Lascio a voi valutare la reazione vincolare (la forza
equilibrante) sul fulcro. |
Un altro tipo di leva, ancora più vantaggioso, lo
realizziamo se poniamo il peso tra la forza attiva e il fulcro.
Questa è una LEVA DI SECONDO GENERE.
Anche qui, per esercizio, calcolatevi rapidamente la reazione
vincolare sul fulcro. |
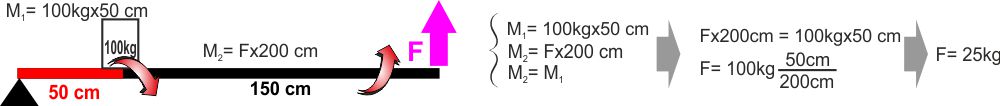 |
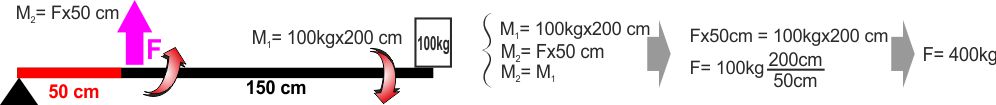 |
Identica alla leva che abbiamo visto prima è invece la
LEVA DI TERZO GENERE, dove abbiamo scambiato il punto di
applicazione della resistenza con il punto di applicazione della
forza attiva. Questa ovviamente è una leva svantaggiosa
(funziona esattamente come la leva di secondo genere, ma al
contrario).
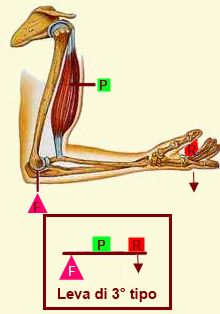
La maggior parte dei nostri muscoli scheletrici (quelli che ci
fanno muovere) agiscono in realtà come leve di terzo genere. |
 |
|
Quindi, in generale, per le leve, abbiamo il
semplice rapporto |
|
|
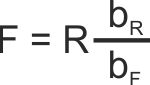 |
| Dove abbiamo indicato con bR
il braccio relativo alla forza resistente e bF
il braccio relativo alla forza attiva. |
|
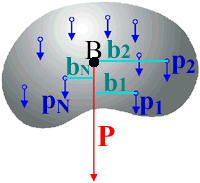
IL BARICENTRO |
Ogni corpo solido presenta un punto particolare, che
è il centro "pesato" della massa di quel corpo.
Vorrebbe dire che se io "appendo" il corpo vincolandolo
esattamente in quel punto questo non ruota.
E' cioè il centro della distribuzione di tutte le forze
di massa (il peso).
E' il punto dove possiamo considerare applicata tutta la
massa (tutto il peso) del corpo.
Se ci calcolassimo tutti i momenti delle forze peso
distribuite come tante piccole masse infinitesime per il
loro braccio rispetto a questo punto troveremmo sempre
che la loro somma è zero. |
 |
|
|
|
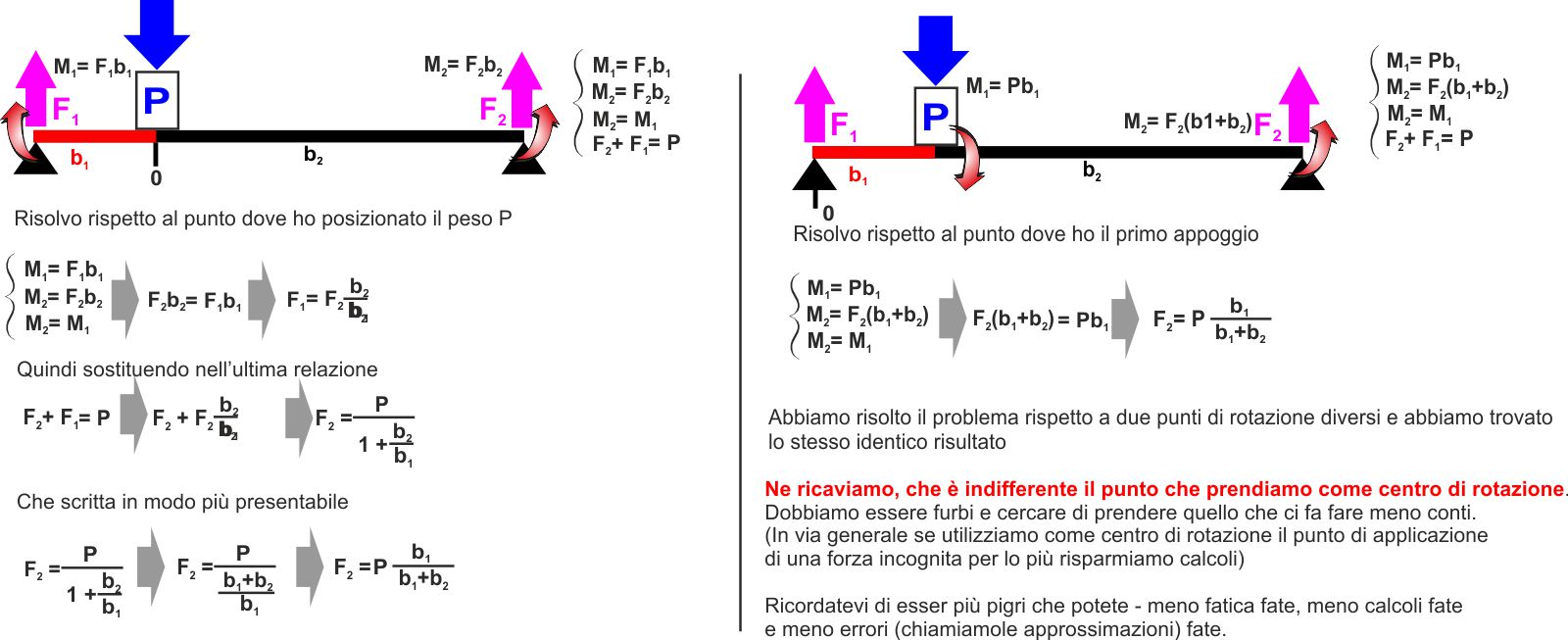
EQUILIBRIO DI UN CORPO SU
DUE APPOGGI |
|
Vediamo i due casi tipici con cui possiamo "bloccare"
una struttura:
Una trave "appoggiata" su due supporti o una trave "incastrata" tra due
supporti.
|
|
|
EQUILIBRIO DI UN CORPO
INCASTRATO |
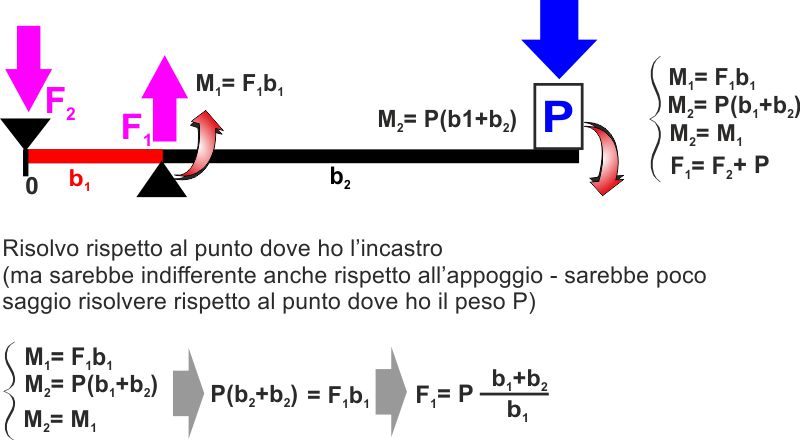 |
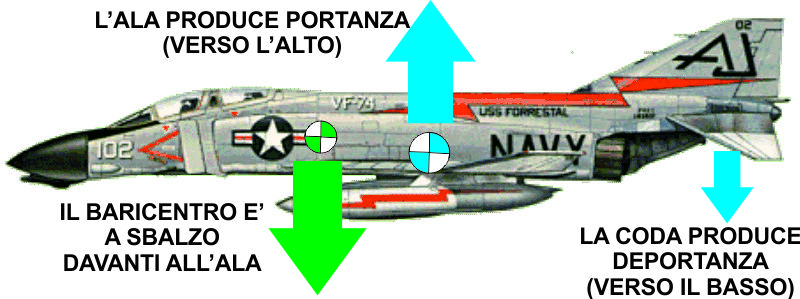
Visto che questo comunque vuole essere un corso di
aeronautica vale la pena notare che gli aeroplani in
configurazione "classica" (piani equilibratori dietro) sono di
fatto travi incastrate.
Cioè l'ala produce portanza (verso l'alto) e la coda deportanza
(tira verso il basso).
|
 |
|
|
|
|
|
|
|
|
|
|

