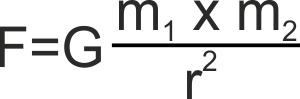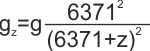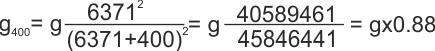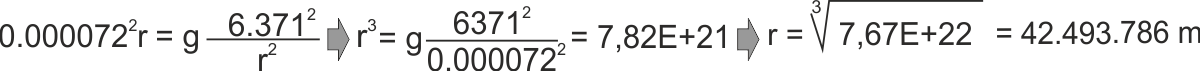Robert Hooke e Isaac Newton negli anni intorno al 1660 spiegarono come
due corpi si attirassero con una forza che era in qualche modo
inversamente proporzionale al quadrato della loro distanza.
Tra le varie ragioni per cui questo sarebbe stato vero c'era la
"necessaria" eguaglianza tra la forza centripeta necessaria a mantenere
in orbita un corpo celeste e l'accelerazione che una traiettoria
circolare a velocità subisce, appunto verso il centro (lo vediamo dopo
quando trattiamo il moto circolare - ho preferito farlo precedere dalla
trattazione della gravitazione perché secondo me il discorso così è più
comprensibile).
Questi due scienziati collaborarono (o quantomeno discussero a lungo in
modo costruttivo) alla stesura di quella che è la "LEGGE DELLA
GRAVITAZIONE UNIVERSALE".
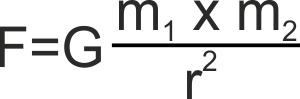
dove :
-
m1 ed m2 sono le
due masse interessate
-
r è la distanza tra queste (immaginate
ridotte ad un punto "centrale")
-
G è una costante universale che "fa tornare i
conti" e vale 6.67408x10-11 m3/kgs2
|

Robert Hooke (1635/1703) |

Isaac Newton (1642/1726) |
|
Il valore di G fu calcolato grazie all'esperimento di
Cavendish nel 1797.
Si prendono due sfere grandi di massa m1 e si fissano
al suolo, poi due sfere più piccole di massa m2 sono
fissate ad una "bilancia di torsione", cioè una bilancia grado di
misurare il momento torcente del filo sottile che a cui è sospeso l'asse
a cui sono fissate le due masse piccole m2.
Le due masse m2 sono attirate con una forza debolissima dalle
masse più grandi m1 ... in pratica con questo sistema si
riesce a misurare la forza che attrae le masse m2 alle masse
m1.
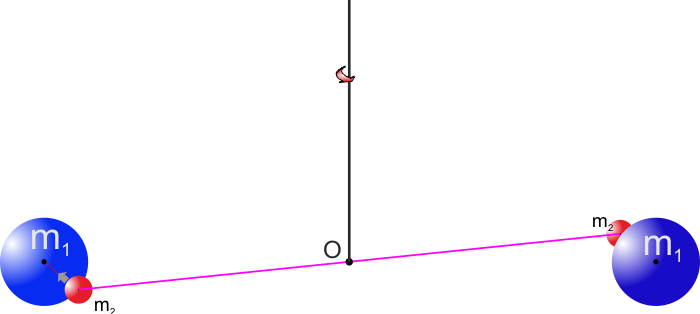 |
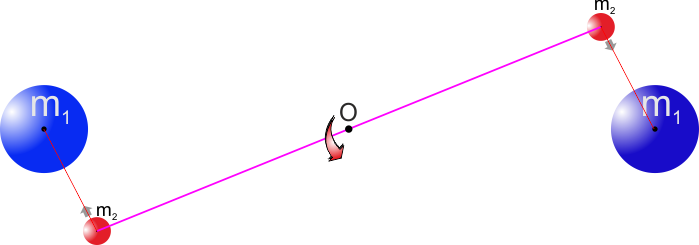
Nell'immagine a lato la bilancia di torsione di Cavendish
vista di fronte e qua sotto la stessa bilancia vista da sopra.
Le due masse m1 sono attirate dalle masse m2
e il filo O "resiste" a questo movimento torcendosi.
Conoscendo il momento torcente sul filo O posso calcolare la
forza che attrae le masse tra loro. |
 |
|
|
Una volta nota la costante G se sostituiamo a r il
raggio della Terra e risolviamo rispetto ad m1 dopo aver
misurato la forza "peso" che si applica ad una massa m2
qualsiasi posta sulla superficie terrestre riusciamo a calcolare la
"massa" della Terra (che è proprio quello che voleva fare Cavendish con
questo esperimento).
Se consideriamo che il raggio della terra è di 6.371 km (raggio medio)
il valore di Gxm1/r2 varia pochissimo anche se ci
allontaniamo dalla superficie terrestre di qualche km e quindi può
essere ragionevolmente considerato costante.
Tale valore è g, l'accelerazione di gravità, che vale più o meno
9,8 m/s2 (vediamo tra poco perché in realtà non è
costante a seconda della latitudine a cui ci troviamo). |
|
A questo punto direi di fare alcune considerazioni
piuttosto semplici ma che probabilmente vanno contro alcune "verità" che
crediamo di conoscere ...
Punto primo : Nello spazio la gravità NON E' ZERO.
Un'astronave o un sasso o qualsiasi cosa sia nello spazio viene attirato
dagli altri corpi. Qui nel nostro sistema solare il più grande di tutti
è il Sole e, grossolanamente, un qualsiasi oggetto "fermo" nello spazio
verrebbe attirato dal Sole.
Il motivo per cui i pianeti, le astronavi, i satelliti, le comete e
insomma tutto quello che si trova nel nostro sistema solare non cade
direttamente nel Sole è perché tutta questa roba si muove velocemente e,
non essendovi attriti nel vuoto, manterrebbe il suo stato di moto
"rettilineo uniforme" all'infinito.
La gravità degli altri corpi celesti però "devia" queste traiettorie e,
se ci sono le condizioni, le trasforma in "orbite", cioè traiettorie più
o meno circolari attorno ad un corpo celeste (i satelliti ruotano
intorno ai pianeti, i pianeti intorno al Sole e, in realtà. tutti questi
oggetti interagiscono tra di loro modificando in modo più o meno marcato
queste "orbite".
Qua sulla Terra, benché siano lontanissime, subiamo comunque
l'attrazione gravitazionale delle Stelle.
|
|
|
|
|
|
|
|
|
|
|
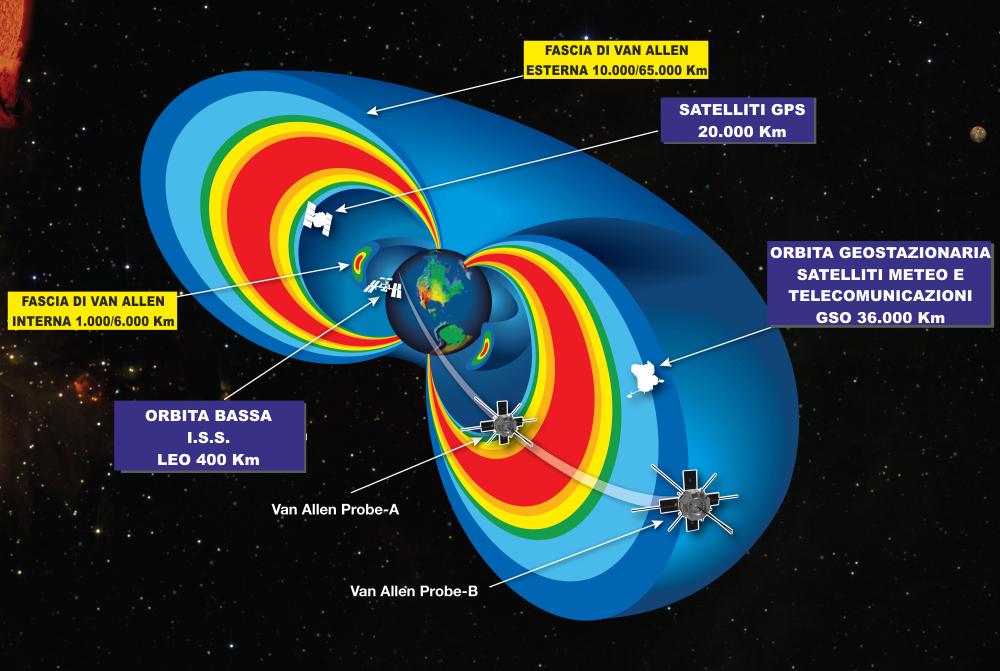
Punto secondo : In orbita la gravità è poco diversa da
quella che abbiamo qua. Ad esempio: la stazione orbitale ISS si trova a più
o meno 400 km dalla superficie terrestre, questo vorrebbe dire che sulla ISS
l'accelerazione di gravità g varrebbe circa il 90% di g ... come ci arrivo?
Semplice: se qui sulla Terra, dove il raggio che devo mettere nella formula
della gravitazione universale è di 6.371 km, ad una distanza z dalla
superficie terrestre l'accelerazione di gravità sarà di 6371+z ..
cioè, genericamente:
|
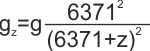
E nel caso della ISS che appunto orbita più o meno a
400 km dalla Terra verrebbe
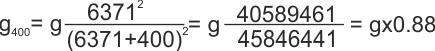
Cioè l'accelerazione di gravità sulla ISS è circa
l'88% di quella che c'è qui (una persona che pesasse sulla Terra 70
kg sulla stazione orbitale ne peserebbe 62).
Ma allora (punto terzo) .. perché la gente che sta
nello spazio "fluttua" in assenza (a questo punto direi "apparente")
di peso?
Perchè si trovano in una situazione di "equilibrio" rispetto
all'accelerazione di gravità che li attira comunque verso la Terra
dovuto alla forza "centrifuga" provocata dalla velocità orbitale.
Detta così può sembrare poco chiara, ma vediamo di semplificare.
|
 |
Ora però, per capire di cosa stiamo parlando dobbiamo
necessariamente introdurre un altro tipo di moto, il moto "circolare
uniforme", cioè la traiettoria di un oggetto che gira a velocità costante
intorno ad un punto.
In una traiettoria circolare la velocità può mantenersi costante in "modulo"
(ad esempio un'auto che affronta una curva a 60 km/h e la mantiene durante
tutta la curva, uscendone ancora a 60 km/h), ma evidentemente cambia di
"direzione" (la velocità è un vettore l'accelerazione è la variazione di
velocità, se questa varia in qualche modo vuol dire che subisce
un'accelerazione).
Intanto semplicemente ragionandoci su (e magari ricordando quello che
abbiamo visto nel paragrafo precedente), se il modulo della velocità
non cambia, cioè se l'oggetto non viene accelerato o rallentato (mantiene i
suoi 60 km/h) occorre che l'accelerazione, se c'è, sia "normale" ovvero
perpendicolare alla sua traiettoria.
In questo modo, come abbiamo visto per il proiettile, il "modulo" della
velocità si mantiene.
Quindi la direzione dell'accelerazione, nel movimento circolare uniforme,
deve essere PER FORZA diretta normalmente alla velocità.
Siccome è ragionevole individuare la velocità istantanea come "tangenziale"
alla traiettoria, è di conseguenza ovvio che l'accelerazione sarà diretta
perpendicolarmente alla tangente e quindi secondo il raggio del cerchio.
A questo punto diventa un pelino più complicato trovare QUANTO vale
l'accelerazione, cioè la variazione di velocità nel tempo.
Intanto facciamo queste considerazioni, puramente "geometriche".
Ricordiamoci cosa sono i "radianti", cioè una unità di misura che si
definisce come l'arco di circonferenza di raggio unitario ...
Ci ricordiamo che la circonferenza è 2 π
r , siccome abbiamo appena detto che la circonferenza che
utilizziamo ha raggio unitario, cioè UNO il valore di tutta la sua
lunghezza (360°) sarà 2 π
e così sarà π
l'angolo di 180° e via così ....
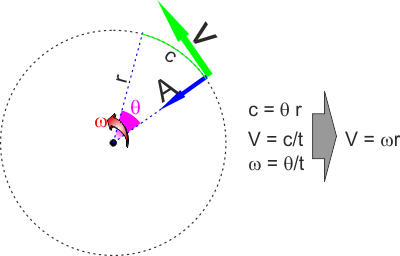
Misurando in questo modo gli angoli un arco di circonferenza
descritto da un arco θ
varrà semplicemente
θr.
Di conseguenza la velocità tangenziale V che sarebbe
θr/t
sarà uguale a ωr
dove con ω
indichiamo la velocità angolare
θ/t. |
 |
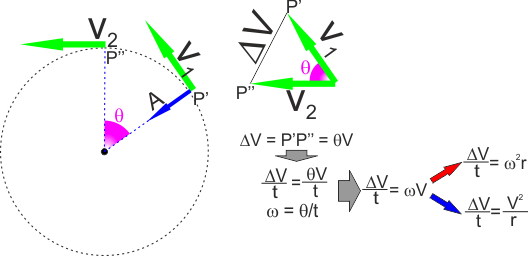 |
A questo punto valutiamo quanto varia la velocità V
nel tempo t ... cioè come cambia il vettore V1 quando si
passa dal punto P' al punto P'' e diventa V2.
Come abbiamo detto prima il "modulo" non cambia, resta sempre V,
mentre cambia la direzione.
La differenza dei due vettori V1 e V2 è ... la
differenza tra i vettori V1 e V2,
semplicemente, cioè il vettore che unisce le punte di V1
e V2.
La differenza di inclinazione tra V1 e V2 è il
solito angolo
θ,
che se lo misuriamo in radianti come abbiamo fatto prima mi da che
ΔV
è uguale a θV.
ΔV / t,
cioè l'accelerazione, variazione di velocità rispetto al tempo, sarà
di conseguenza θV/t
o, più semplicemente, ricordando che abbiamo definito la
velocità angolare ω=
θ/t,
ωV.
La forma ωV
è però "bruttina a vedersi" e in generale poco pratica da
utilizzare ... ricordandoci dell'equivalenza V=
ωr
che abbiamo visto prima diventa, e seconda di come ci viene più
comoda:
Ac=
ω2r
oppure Ac=
V2/r
Il pedice c di Ac sta a
ricordarci che parliamo di accelerazione rivolta verso il centro
della traiettoria e cioè "centripeta". |
Fatto questo torniamo alla nostra forza di gravità e alla
roba che gira in orbita.
A questo punto è "facile" valutare i parametri di un'orbita ... data la
quota si trova la velocità o data la velocità si trova la quota, è solo
questione di fare calcoli.
Vediamo due casi ... valutiamo la velocità di un satellite che debba stare
ad una certa distanza dalla Terra.
Come abbiamo visto prima la "forza di gravità" che lo "tira" verso il centro
della Terra è
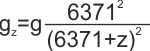 e,
giusto per non fare altri conti, per la ISS diventava e,
giusto per non fare altri conti, per la ISS diventava
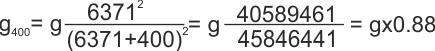
Quindi l'accelerazione di gravità a 400 km dalla superficie
terrestre è di 0.88g ovvero (visto che g vale 9.8 m/s2) 8.62 m/s2.
Questa accelerazione deve essere perfettamente uguale a quella che serve per
mantenere il moto circolare uniforme della ISS, quindi 8.62 = V2/r
con r che è di nuovo il raggio della Terra più i nostri 400 km
(nota: siccome esprimiamo l'accelerazione e la velocità in m/sec2
e in m/sec occorre riportare in m anche tutte le altre misure).
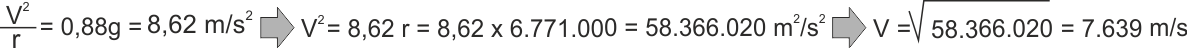
7.639 m/s cioè circa 27.500 km/h.
Facciamo una altro caso .. cioè la situazione nella quale vogliamo che il
satellite stia in orbita "geostazionaria", cioè orbiti "sincrono" con la
Terra (sono i satelliti per le telecomunicazioni o meteorologici, che devono
restar sempre nello stesso punto rispetto ad un osservatore che li "punti"
dalla Terra.
Ammettendo (non è preciso) che la Terra compia un giro ogni 24 ore la sua
velocità (angolare, questa volta) sarà di 15°/h (360°/24= 15°) - che
sono 0.004°/sec o ancora 0.000072 rad/sec.
Avremmo quindi che la accelerazione centripeta DEVE essere 0.0000722
x r
La gravitazione terrestre, oramai lo abbiamo capito, ci fornisce
un'accelerazione g ad una distanza di 6.371 km dal centro (della
Terra).
Questa volta, siccome dovremo risolvere rispetto da r non ci conviene
utilizzare la formula che ci dava gz con z la distanza dalla
superficie terrestre, ma direttamente una z che sia la distanza dal centro
della Terra (poi ci toglieremo il raggio terrestre, che tanto è costante,
una volta ottenuto il risultato).
In questo modo avremo
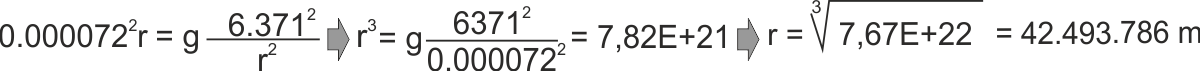
Cioè che per stare in orbita geostazionaria qualsiasi
satellite, qualsiasi massa abbia, qualsiasi forma e funzione abbia, deve
stare esattamente a 42.493 km dal centro della Terra.
Togliamoci i 6.371 km del raggio terrestre e viene fuori che i satelliti
geostazionari orbitano a 36.000 km sopra le nostre teste.
E a che velocità? ... A questo punto direi che il conto è facile, 0.000072
rad/sec x 42.000 km .. cioè 3.024 m/sec ... 10.888 km/h.
A questo punto farei una considerazione:
Siccome abbiamo visto che per orbitare vicino alla Terra occorre andare "più
veloce", mentre se siamo lontani dobbiamo andare più lenti .. e
l'accelerazione centrifuga è proporzionale alla velocità al quadrato ...
vuol dire che data una certa posizione dobbiamo avere una velocità ben
precisa per restare in orbita.
Se siamo più lenti cadremo sulla Terra, mentre se siamo più veloci ci
allontaneremo nello spazio.
Questo è il motivo per cui le migliaia di asteroidi che passano vicino alla
Terra è praticamente impossibile (ovvero fortissimamente improbabile) che
transitino ad una distanza e velocità tali da restare in orbita intorno al
nostro pianeta.
Se sono troppo lenti cadono sulla Terra, se sono troppo veloci si
allontanano. Dovrebbero avere una velocità ben precisa e passare ad una
distanza ben definita per essere "accalappiati" e diventare un "satellite"
della Terra.
| MA ... un momento ... ma se noi siamo sulla superficie della
Terra anche noi abbiamo una velocità di "rotazione" attorno al
centro della Terra che vale la
ω che
abbiamo calcolato prima - l'accelerazione che ne consegue
(centrifuga, stavolta, cioè la parte di accelerazione che viene
"compensata" dalla nostra velocità) vale
ω2r
dove r più che il raggio terrestre è la distanza del punto dove
ci troviamo rispetto all'asse di rotazione terrestre (è uguale al
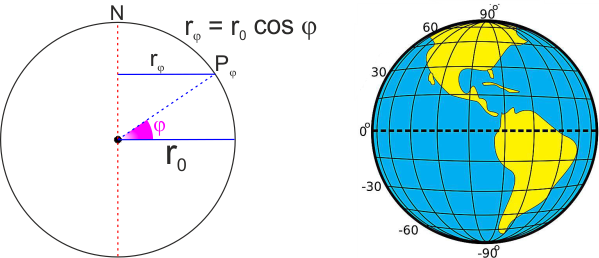
raggio terrestre solo all'equatore). Questa velocità vale, come si è
detto, 0.000072 rad/sec e l'accelerazione che ne consegue, per un
punto posto alla latitudine
φ,
guardando la figura, sarebbe :

Il che vorrebbe dire, grossolanamente, che una
persona che al polo pesasse 60 kg all'equatore peserebbe 60/9.8 x
(9.8-0.033)
cioè 59.79 kg ... insomma, se vi spostate dal polo all'equatore la
bilancia vi abbuona un paio d'etti ogni 60 kg. |
 |
|