Fisica - dispense
Moto uniformemente accelerato

1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
 
Riprendiamo i concetti dell'ultimo capitolo, ricordando l'equazione oraria del moto "uniformemente accelerato" che nella sua forma "completa" è:

Dove :

  • L0 è la posizione iniziale (che non deve essere necessariamente "zero")
  • V0 è la velocità iniziale (quella che il corpo possiede nell'istante iniziale - non è detto che il nostro corpo parta "da fermo")
  • A è l'accelerazione a cui il corpo è sottoposto

Nei casi pratici che valuteremo da qui in avanti l'accelerazione sarà quella di gravità e cioè g = 9.8 m/s2
Di conseguenza l'equazione di cui prima diventa:

Bene - cominciamo a vedere come applicare in modo "interessante" questa equazione ...
Primo problema :

Lascio cadere una pietra dal secondo piano di un edificio (circa 8 metri) ... quanto impiega a toccare terra?
Applichiamo l'equazione del moto, che nel nostro caso vedrà nulli sia L0 che V0 (il sasso parte da fermo e conto lo spazio "a scendere").

Risolviamo rispetto a t (è la stessa cosa che abbiamo fatto nel paragrafo precedente) mettendo al posto di g il suo valore di 9.8 m/s2 e al posto di h il valore di 8 metri.

Poi già che ci siamo calcoliamoci la velocità con la quale il sasso impatta al suolo ...
Banalmente se l'accelerazione è costante sarà V=gt con g sempre 9.8 m/s2 e t 1.27 secondi come abbiamo appena calcolato
Viene una velocità di 12.44 metri al secondo ...
Per curiosità riportiamola in km/h .. in un minuto ci sono 60 secondi e in un'ora 60 minuti, quindi 12.44 x 60 x 60 ...
Vengono 46 km/h .
Che è più o meno la velocità cui vanno i "cinquantini", cioè i motorini che si possono guidare a 14 anni.
Dai conti appena fatti si vede che se andiamo a sbattere con un cinquantino contro un muro subiamo lo stesso effetto che se ci buttassimo dal terrazzo di un secondo piano . E così oltre a "fisica" abbiamo anche visto qualcosa sulla validità delle regole del codice stradale. 40 km/h sembrano pochi ma .. in realtà tanto tanto pochi non sono.
Ora rivediamo il problema dello scorso capitolo ... non aggiungiamo assolutamente nulla, ma è giusto perché è in questo che vogliamo trattare il moto uniformemente accelerato e quello era un altro caso tipico.
Quello che qui voglio rimarcare è l'indipendenza del moto orizzontale rispetto a quello verticale.
E' roba che dovremmo aver fatto l'anno scorso .. con i vettori.
Fatta o non fatta, secondo il primo principio della dinamica un corpo se non è soggetto a forze mantiene il suo stato di moto rettilineo uniforme.
Se consideriamo il proiettile sparato dal cannone, il suo moto in senso orizzontale in effetti non viene"perturbato" da nessuna forza, perchè la forza di gravità lo accelera si, ma in direzione perpendicolare a quella del moto iniziale, quindi LUNGO L'ASSE ORIZZONTALE il moto si mantiene a velocità uniforme.
Se Vx era la sua velocità in uscita dalla bocca del cannone lui continuerà a viaggiare a quella velocità nella direzione "orizzontale".
Cioè la sua velocità cambierà, ma la componente orizzontale resterà inalterata.
In direzione "z" cioè verticale, invece, il suo moto sarà identico a quello di un sasso lasciato semplicemente cadere dalla stessa altezza.
Quindi, come abbiamo appena visto

Cioè il proiettile "sta in aria" per il tempo t, che se la torre fosse alta, ad esempio, 15 metri, sarebbe 1.74 secondi.
In quel tempo il nostro proiettile (supponiamo sia stato lanciato a 100 m/sec) percorre 174 metri.
E se invece volessimo fare un "salto" in lungo?
Ad esempio, supponiamo di voler fare un salto con la moto ...
Ovviamente non possiamo saltare semplicemente in orizzontale, perché per poco che saltassimo la nostra moto comunque un po' scenderebbe, come la palla del cannone vista prima.
Per fare il salto dobbiamo attrezzarci una pedana inclinata in modo da saltare con un certo "angolo di rampa" α.
Quindi la nostra moto si muove a velocità V su una rampa inclinata.
Scomponiamo la velocità nelle due componenti Vz1 e Vx rispettivamente sull'asse "Z" verticale e sull'asse "X" orizzontale.
Per fare questa scomposizione dobbiamo utilizzare le "funzioni trigonometriche". Se non le conosciamo possiamo semplicemente "fidarci" oppure andare a vedere rapidamente cosa sono.

Come è riassunto in figura Vz1 vale V sen α mentre Vx è V cos α.
Poi facciamo come prima ... Vx non varia, resta costante (occhio, in realtà varia a causa della resistenza dell'aria, ma qui la trascuriamo ...), mentre in senso verticale abbiamo l'accelerazione di gravità g che agisce sulla nostra moto, che però stavolta è dotata di una velocità iniziale Vz1.
La "legge del moto" nel senso dell'asse Z diventa


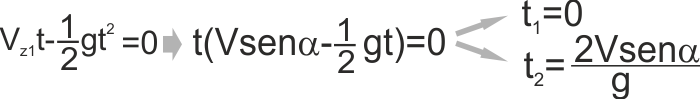
Uguale a zero perché supponiamo che il punto in cui la moto "stacca" sia alla stessa quota della rampa dove poi intendiamo atterrare, se così non fosse dovremmo metterci dentro anche una costante "h" che però qui non voglio considerare per semplice pigrizia .. se no l'equazione diventa completa di secondo grado e risolverla diventa più complicato. E' un esempio, facciamolo semplice.
Come si vede porre lo spazio uguale a zero comporta due soluzioni: una per t1=0 ... lo sapevamo già, nel momento in cui la moto lascia la rampa la sua quota è "zero" ed è da quell'istante che cominciamo a misurare il tempo.
L'altra per t2= 2Vsen α /g
Lo spazio che percorreremo sarà quindi la Vx che era Vcos α moltiplicata per questo tempo t2 .

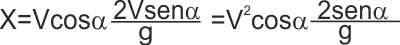
Sembra una cosa difficile, ma in realtà non lo è per niente ...
Basta mettere dei numeri e tutto si semplifica ...
Ad esempio supponiamo che la nostra rampa abbia un'inclinazione di 30° sull'orizzontale ...

  • sen 30° = 0.5

  • cos 30° = 0.866

  • g = 9.8 m/s2

Il salto verrebbe lungo 0.09 V2

Se la nostra moto andasse a 100 km/h (che in metri al secondo fa 100.000/3600= 27.77 m/s) il salto sarebbe lungo 46 metri ...
Più o meno 38 auto parcheggiate, se volete provare ..

Per saltare una distanza prefissata ... ad esempio 10 auto, circa 12 metri, dobbiamo fare il calcolo al contrario

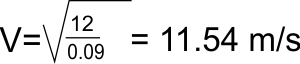
Che riportata in km/h fa 11.54x3600/1000=41.54 km/h ... cioè per saltare 10 auto ci basta il motorino ...
Ovvio che non è un esperimento da fare, anche perché qui non abbiamo considerato la resistenza dell'aria, che rallenta la nostra Vx con una forza "aerodinamica" che è funzione di V2 (più o meno 1/2 ρ V2 S CD, dove ρ è la densità dell'aria, S la superficie della sezione "frontale" di moto più motociclista e CD un coefficiente di resistenza che bisognerebbe trovare sperimentalmente con prove in galleria aerodinamica).
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20