In realtà li abbiamo già incontrati, almeno per un paio
di questi.
Il PRIMO PRINCIPIO della dinamica dice che un
corpo sottoposto a nessuna forza (o ad un sistema di
forze a risultante nulla) mantiene il suo stato di moto
rettilineo uniforme.
Questo concetto, per quanto a noi oggi familiare, non è in
realtà così semplice da intuire, tanto è vero che per secoli
si studiò quanto descrive Aristotele, e cioè che lo stato
naturale di un corpo è la quiete (un oggetto, per quanto io
possa spingerlo o lanciarlo, se lo lascio andare prima o poi
si ferma).
Chi contestò questa apparente evidenza fisica fu Galileo
Galilei, che sperimentando il moto di sfere metalliche su
"piste" di legno si accorse che più le piste erano lisce e
più lontano andavano le sfere .. giungendo alla conclusione
che se non ci fosse stata una qualche forza che in qualche
modo dipendeva dalla finitura delle sue piste di legno, le
sfere avrebbero continuato a rotolare indefinitamente.
|
 |
 |
Lo stesso Galileo inventò il telescopio, con il quale
poté osservare il cielo e in particolare si accorse che
intorno a Giove c'erano dei sassolini che ruotavano
all'infinito ... (i suo satelliti, i primi 4 scoperti, detti
appunto Galileiani: Io, Europa, Ganimede e Callisto).
Per questo Galileo pensò che in realtà la condizione
"normale" di un oggetto non sottoposto ad alcuna forza fosse
il moto circolare uniforme.
Come però abbiamo visto nel capitolo precedente in realtà
questa condizione è dovuta alla presenza della forza
gravitazionale di Giove che fornisce l'accelerazione
centripeta che fa deviare il moto rettilineo e lo trasforma
in circolare (lo abbiamo visto nel
capitolo precedente, non per Giove ma per la Terra -
ovviamente le considerazioni valgono per qualsiasi altro
corpo celeste e non).
Non voglio qui complicare le cose, ma in effetti il "moto
rettilineo" che potremmo sperimentare sulla Terra, ad
esempio facendo rotolare una sfera su una pista piana
infinita, in realtà sarebbe un moto circolare (visto che la
Terra è sferica la pista che ci appare piana in realtà è
curva).
Newton raccolse questo principio e gli altri due che stiamo
per enunciare nella sua opera "I principi matematici della
filosofia naturale" del 1687 (all'epoca "filosofia naturale"
e "fisica" erano sinonimi).
Il SECONDO PRINCIPIO della dinamica afferma che la
variazione del moto di un corpo (cioè la sua accelerazione)
è proporzionale alla forza ad esso applicata o, in modo
semplice ed esplicito |
|
F=ma
Dove :
- F è la forza applicata al corpo
- m è la massa del corpo
- a è l'accelerazione cui il corpo è sottoposto
a causa della forza F
Giusto per precisare, seppure ovvio, visto che
l'accelerazione è un "vettore" e la massa uno "scalare"
forza e accelerazione avranno stessi direzione e verso.
Le dimensioni della forza sono quindi massa per
accelerazione cioè kg x m /s2
L'unità di misura è il NEWTON, definito come la
forza che accelera di un m/s2 la massa di un kg. |
 |
 |
|
Il TERZO PRINCIPIO della dinamica o principio di
"AZIONE/REAZIONE" dice che se un corpo A esercita una
"forza" F su un corpo B "istantaneamente" (o se preferite
"contemporaneamente") il corpo B esercita una forza identica
ma di direzione opposta sul corpo A.
Che esperienza abbiamo di questo?
Proviamo a spingere una cassa ... si sposta la cassa.
Proviamo a spingere la stessa cassa indossando dei pattini a
rotelle ... ci spostiamo noi ...
La forza esercitata è la stessa, e in realtà anche quando si
sposta la cassa, noi (e la Terra con noi) un pochino ci
spostiamo all'indietro, ma essendo "solidali" con la Terra
la nostra massa in realtà è la somma della massa della Terra
più la nostra e così la nostra accelerazione diventa
ridicolmente piccola.
Idem, all'opposto, quando è la cassa a non spostarsi. |
 |
 |
 |
Facciamo un altro esempio, più calzante ma meno
"immediato" da capire (ne ho viste di persone finire in
acqua perchè quello che andiamo a vedere non è così
"immediato" al nostro istinto ...).
Se siamo su una piccola imbarcazione leggera (un canotto o
una canoa, ad esempio, NON LEGATA) e ci spostiamo in avanti
per raggiungere il molo ... noi ci spostiamo in avanti e la
canoa si sposta all'indietro ...
La forza che noi esercitiamo credendo di fare un passo in
avanti in realtà "spinge" la canoa all'indietro ...
Siccome noi ci spostiamo in avanti e la canoa all'indietro
con la stessa forza è m1a1=-m2a2
Dove con m1 ed m2
indichiamo le masse nostre e della canoa e con a1
e a2 le corrispondenti accelerazioni ... |
Se volessimo fare due conti (ad esempio vedere quanto vale
l'accelerazione della canoa) si vede facilmente che a2=-a1
m1/m2 o anche a2/a1=-m1/m2
Cioè che il rapporto tra la nostra accelerazione e quella della
canoa è uguale al rapporto tra la massa della canoa e la nostra.
Possiamo pensarla anche così ... se siamo in un sistema "chiuso"
nulla di quello che possiamo fare all'interno di questo sistema può
far accelerare l'intero sistema.
Siccome l'accelerazione dopo un po' si trasforma in velocità
(matematicamente a x t = v) ...
così come vale la relazione m1a1=-m2a2
possiamo considerare che valga anche
m1v1=-m2v2
Il prodotto di massa per velocità spesso è più facile da
utilizzare nei calcoli e prende il nome di "QUANTITA' DI MOTO".
Visto così si potrebbe dire che se produco una certa quantità di
moto in un senso "automaticamente" se ne deve produrre una identica
in senso opposto.
O ancora, che la quantità di moto totale dell'universo (che nel suo
piccolo è un sistema chiuso) è costante (se spingo qualcosa in
avanti qualcos'altro deve andare indietro).
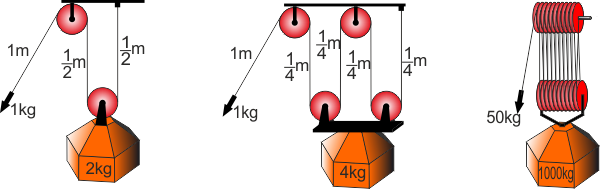 |
Vediamo immediatamente un'applicazione pratica molto
utile ... supponiamo di voler sollevare un peso Q molto
grande (ad esempio una tonnellata) ma avere a disposizione
solo il nostro piccolo fisico con una capacità di
sollevamento di 50 kg ... come possiamo fare?
Possiamo utilizzare un meccanismo noto come "paranco"
... Funziona così:
Se io sollevo un carico che è collegato ad una fune tramite
una carrucola come indicato in figura ogni metro di corda
che io recupero corrisponde al sollevamento del carico della
metà (mezzo metro) o se volete io tiro la mia corda di un
metro al secondo e sollevo il carico di mezzo metro al
secondo ... rispettando la conservazione della quantità di
moto, tanto ne produco verso il basso e tanto se ne alza ...
alla metà della velocità sollevo il doppio del peso.
Quindi con una forza di 50 kg e un sistema di questo tipo
solleverò 100 kg ... ma se raddoppio le carrucole (faccio
passare di nuovo la corda su una seconda carrucola collegata
al carico e su un'altra fissa) ogni volta che tiro un metro
il mio carico si alzerà di soli 25 cm .. e i miei 50 kg
solleveranno 200 kg !!!
Se voglio sollevare 1000 kg? Occorre che il peso si sollevi
solo di un ventesimo del cavo che io ho fatto scorrere ...
Quante carrucole servono? |
Ogni "filo" si deve accorciare ovviamente della stessa quantità,
e la somma dei tratti di cavo guadagnati su ogni filo è uguale
all'avanzamento del cavo principale ... quindi se voglio sollevare
un peso 20 volte la forza che posso applicare per sollevarlo ....
dovrò realizzare un paranco con 20 cavi e quindi 10 carrucole mobili
e 10 fisse .
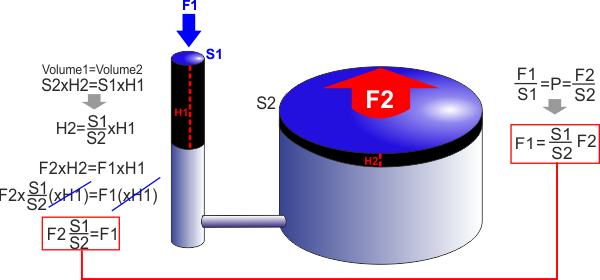
Vi ricordate il "torchio idraulico" ? Avevamo visto come
applicando una forza F1 su una pistone con sezione S1
collegato tramite un tubo ad un cilindro con un altro
pistone di sezione S2 si otteneva una forza F2 tale che
F2=F1 x S2/S1.
Questo perché la pressione P1 (F1/P1) sul pistone di sezione
S1 doveva essere uguale alla pressione P2 sul pistone di
sezione S2 e quindi F2 sarebbe stato P1xS2.
Però possiamo vedere la cosa esattamente come la questione
paranco ... il pistone di sezione S1 per far sollevare il
pistone di sezione S2 di un centimetro deve muovere un
volume di fluido uguale ad un cm x S2 .. ma per farlo deve
spostarsi di un valore S2/S1 cm ... cioè alla fine sollevo
un peso S2/S1 volte la forza che applico di un cm se sposto
il mio pistone di S2/S1 cm.
In soldoni se voglio sollevare un peso 10 volte più grande
della forza che posso applicare devo avere un secondo
pistone 10 volte più grande del primo, ma siccome mantengo
il volume del fluido nei due cilindri il primo pistone
scende 10 volte di più di quanto non salga il secondo. |
 |
Abbiamo fatto un po' di confusione tra forze e masse ? Tra
velocità e spostamenti ?
Per quanto possa sembrare poco serio ... alla fine ... è lecito ...
Forza per spostamento è energia, e anche quella si mantiene (lo
vediamo nel prossimo capitolo).
Forza per velocità è potenza, che è variazione di energia nell'unità
di tempo .. se istante per istante si mantiene l'energia allora si
mantiene anche la potenza.
Se invece di una forza che spinge consideriamo una massa che si
abbassa e una che si alza ricadiamo nel discorso quantità di moto
... |
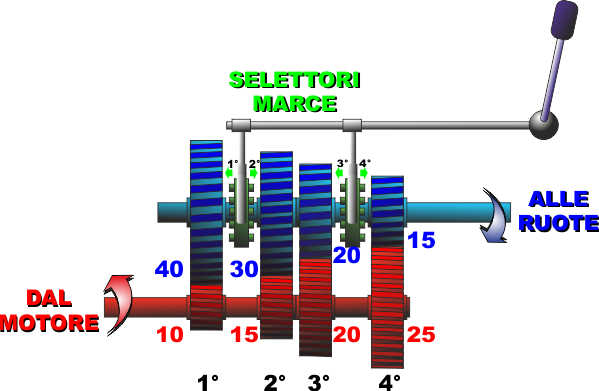 |
Vediamo ancora un'altra applicazione di questi concetti : il cambio
dell'automobile.
Qui manteniamo la "potenza" data dal motore sino alle ruote,
passando per un movimento di rotazione e quindi avremo a che fare
con velocità angolari e momenti di forze.
Come funziona il cambio di un'auto?
E in generale come faccio a trasformare una piccola forza applicata
ad una cosa che si muove velocissima (il pistone nel cilindro fa
tipo 6000 cicli al minuto) in una grande forza (in grado di spostare
il peso di un'auto) per un movimento relativamente molto più lento?
Semplice ... faccio girare veloce una piccola ruota applicandoci una
piccola forza (momento) e questa la collego ad una più grande ...
dovendo corrispondere le velocità tangenziali (le ruote si toccano
sul bordo) le velocità angolari saranno in "rapporto" alle
circonferenze delle ruote dentate. |
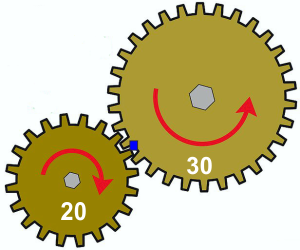 |
Anzi, siccome i denti devono ingranare uno
nell'altro, ancora più semplicemente il "rapporto" tra le
velocità angolari delle ruote sarà nello stesso rapporto tra
il numero dei denti di una e dell'altra.
In rapporto inverso avremo il "momento" ... ovvero la
"forza" sull'asse.
Capisco che il concetto possa essere un po' nebuloso, forse
meglio descriverlo con un esempio.
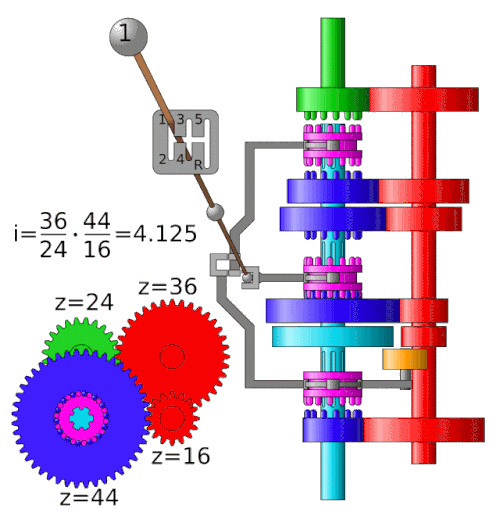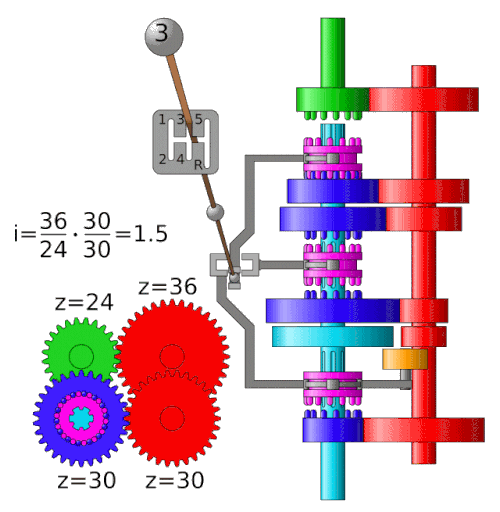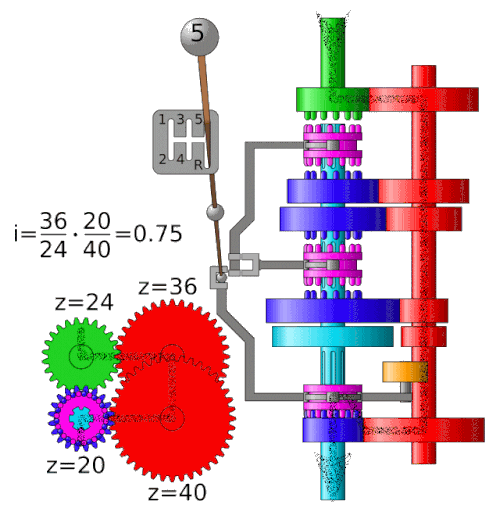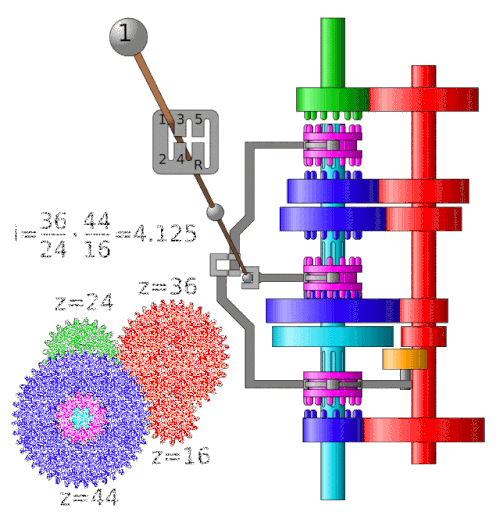
Nel caso del cambio rappresentato a lato (4 marce) avremo
che:
in 1° la ruota che trasmette la potenza ha 10 denti e la
ruota che la riceve 40, per cui la velocità angolare
ω1
sull'albero che va alle ruote sarà 1/4 della velocità
angolare ω2
dell'albero motore, allo stesso tempo il "momento" sull'asse
di trasmissione sarà 4 volte quello all'asse motore.
Infatti utilizziamo la 1° marcia a basse velocità e alti
sforzi (per partire, quando dobbiamo accelerare il veicolo
da zero o eventualmente in salite molto inclinate, quando
abbiamo bisogno di una grande "forza" per vincere la forza
di gravità e "sollevare" il peso dell'auto. |
|
 |
 |
Un cambio come quello raffigurato qua sopra
(sincronizzato a 4 marce) funziona più o meno così:
Le 4 ruote dentate rosse sono collegate solidali all'albero
motore (in verità subito a monte ci sarebbe un riduttore -
cioè un altro ingranaggio - e la frizione, ma questo esula
dagli scopi del nostro esempio), e fanno girare le 4 ruote
dentate blu, che invece sono "libere" rispetto all'asse che
poi va alle ruote (alla trasmissione e al differenziale).
Con la leva del cambio faccio scorrere i due selettori che
sono solidali all'asse di trasmissione e che vanno ad
"agganciare" una delle 4 ruote dentate, "ingranando" la
marcia selezionata.
A seconda del rapporto del numero di denti tra la ruota "conduttrice"
(che è quella collegata all'albero che fornisce la potenza)
e quella "condotta" (che è quella collegata
all'albero che utilizza la potenza), avremo un rapporto di
velocità e di momento (coppia) tra l'albero motore e quello
di trasmissione.
Per il cambio rappresentato qui sopra i rapporti sono quelli
nella tabella a lato. |
|
|
|
Sul principio di "azione/reazione", cioè sul terzo
principio della dinamica, si basa anche il funzionamento dei
motori a getto o a razzo.
Nel caso del motore a getto si "aspira" aria dall'esterno e
si accelera all'indietro, ottenendo una "spinta" in avanti
del velivolo.
Nel motore a getto prendiamo aria dall'esterno, quindi il
nostro a"sistema chiuso" è un po' più difficile da trattare.
E' invece molto più semplice vedere cosa succede nel caso di
un motore a razzo.
Il principio è quello del palloncino ... noi lo gonfiamo e
poi lo lasciamo andare .. l'aria esce dal foro e il
palloncino viene spinto in direzione opposta.
I velivoli spaziali lavorano nella stessa maniera.
Hanno un serbatoio che contiene un "qualcosa" che buttano
fuori all'indietro, spingendo in avanti l'astronave.
Di solito utilizziamo ossigeno e idrogeno, che quando si
combinano insieme producono calore (combustione) che fa
aumentare enormemente la temperatura e quindi il volume del
gas (quello che esce alla fine è vapore acqueo), aumenta la
temperatura e quindi il volume, e il gas esce a grande
velocità.
La spinta del razzo sarà uguale alla massa del gas espulso
per la sua accelerazione, o, se ci sembra più semplice, il
nostro razzo si muoverà con una velocità tale da mantenere
costante la somma delle "quantità di moto" (butto fuori m2
gas a velocità v2 e il mio razzo di massa m1
si muoverà alla velocità v1 tale che m1v1=m2v2).
Quindi, in assenza di forze gravitazionali (quindi nello
spazio libero, sufficientemente lontani da pianeti o
stelle), la velocità a cui possiamo sperare di far andare la
nostra astronave è data dalla velocità alla quale siamo in
grado di espellere il gas (ma anche qualsiasi altra cosa
abbia una massa) moltiplicata per il rapporto tra la massa
espulsa e la masse dell'astronave che vogliamo spostare.
Va da se che se potessimo "fissare" il centro di gravità del
sistema "razzo+gas", questo resterebbe fermo
indipendentemente dal modo in cui si dovesse muovere il
razzo.
Ricordiamoci infatti che L (spazio .. lunghezza) = Vxt.
|
 |
|
|
 |
| |
|