Cominciamo con una semplice "analisi" della rappresentazione del moto.
Nel grafico della figura qui sotto abbiamo messo in relazione lo spazio
percorso nel tempo da 5 auto da corsa, vediamo cosa vuol dire.
La prima cosa che dobbiamo ben chiarire è che le traiettorie sono "unidimensionali",
cioè le auto vanno in una direzione fissa.
Leggiamo quello che succede in funzione del tempo, cioè partiamo da "t0"
e poi t1, t2, t3 ....All'istante t1
le auto arancio e rossa partono dalla stessa posizione, l'auto blu è più
avanti. la verde ancora più avanti e la gialla davanti a tutti.
Man mano che passa il tempo vediamo che:
- Il veicolo blu non cambia la sua posizione - è fermo
- Il veicolo giallo diminuisce la sua distanza dal punto di
partenza ... sta andando in retromarcia
- Il veicolo arancio appare subito essere il più veloce di tutti
- I veicoli rosso e verde non modificano la loro distanza nel
tempo, quindi viaggiano alla stessa velocità
|
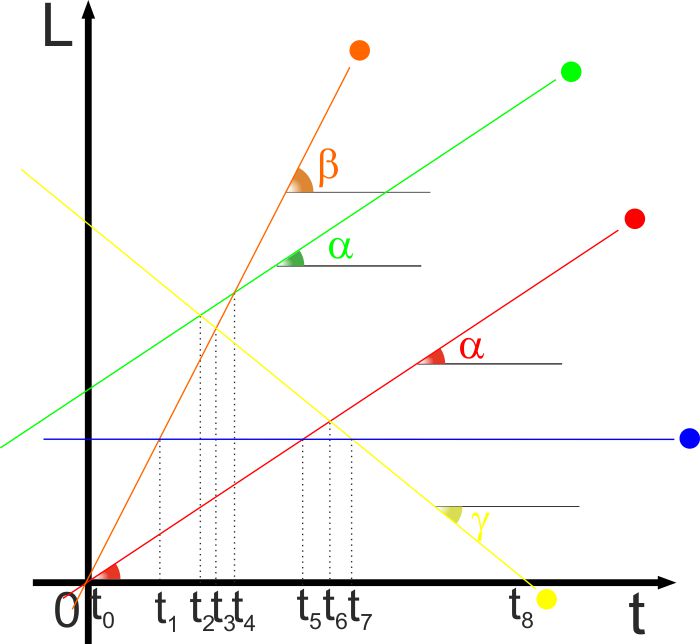 |
- All'istante t0 il veicolo arancio e il
veicolo rosso sono nella stessa posizione, ma è
immediatamente evidente che il veicolo arancio è più veloce
- All'istante t1 il veicolo arancio raggiunge
il veicolo blu
- All'istante t2 il veicolo verde raggiunge il
veicolo giallo che sta retrocedendo
- All'istante t3 il veicolo arancio raggiunge
il veicolo giallo
- All'istante t4 il veicolo arancio raggiunge e
supera il veicolo verde
- All'istante t5 il veicolo rosso raggiunge il
veicolo blu
- All'istante t6 il veicolo rosso raggiunge il
veicolo giallo
- All'istante t7 il veicolo giallo raggiunge in
retromarcia il veicolo blu fermo
- All'istante t8 il veicolo giallo è
arretrato sino alla linea di partenza
|
 |
|
Ora dobbiamo definire alcune cose .. se non abbiamo problemi con i
concetti di spazio (monodimensionale, cioè una sola direzione, lo
misuriamo come la semplice distanza dal punto di partenza) e di tempo,
dobbiamo invece definire il concetto di "velocità".
Per essere precisi definiamo velocità il rapporto tra lo spazio percorso
e il tempo impiegato per percorrerlo
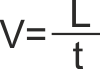
O meglio ancora lo spazio percorso nell'unità di tempo
(infatti quando l'unità di tempo è il secondo saranno metri al secondo o
km all'ora se l'unità di tempo che vogliamo usare è l'ora) |
 |
In tutti i casi che abbiamo visto sopra le velocità erano costanti, cioè
le nostre auto si muovevano di MOTO RETTILINEO UNIFORME
Qualitativamente potevamo dire che :
- La velocità dell'auto gialla è negativa (va all'indietro) e
quindi il rapporto L/t è negativo
- La velocità dell'auto blu è nulla (l'auto sta ferma), il
rapporto L/t è uguale a zero
- Le due auto verde e rossa vanno alla stessa velocità (la loro
distanza non cambia nel tempo) e quindi i rapporti L/t sono uguali,
cambia il punto di partenza
- L'auto arancio va più veloce delle altre (il rapporto L/t è più
grande che per le altre auto)
L'anno scorso abbiamo visto, facendo matematica, che una figura ce si
possa esprimere con l'equazione Y=kX+c è una retta, che il valore c è il
"termine noto" e che qui rappresenta semplicemente la posizione delle
auto al momento della partenza, istante t0.
Che, a parte il termine noto, il valore di k (coefficiente angolare
della retta) che esprime il rapporto tra Y e X (per noi tra L e t) è in
qualche modo legato all'angolo che la retta forma con l'asse delle X
(per noi con l'asse t). Più è grande questo valore e più è grande
l'angolo, e come abbiamo intuito sin da subito, più la retta è ripida e
più l'auto va veloce.
Quello che abbiamo visto sino adesso è che possiamo rappresentare in un
grafico lo spazio percorso in funzione del tempo e che SE la figura che
ne viene fuori è una retta, allora la velocità è costante.
Oppure, se preferite, se un corpo si muove di moto rettilineo uniforme,
la sua velocità è costante e, come è ovvio, viene rappresentata in un
grafico VELOCITA' / TEMPO come una linea parallela all'asse t (l'asse
delle X).
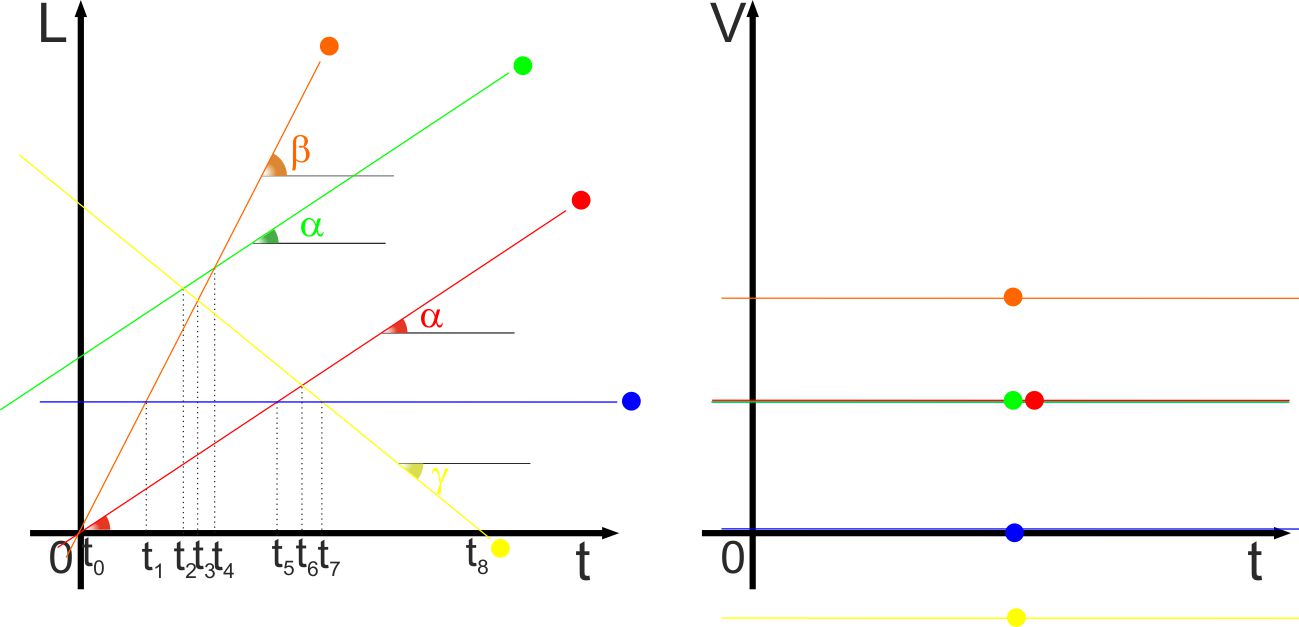
Cosa succede però quando cambia la velocità?
Il moto non è più rettilineo uniforme, caratterizzato appunto da
velocità costante, ma diventa "accelerato".
Come la velocità è la variazione dello spazio rispetto al tempo
esattamente nello stesso modo possiamo vedere l'accelerazione come la
variazione della velocità rispetto al tempo.
Negli esempi di prima, con velocità costante, l'accelerazione sarebbe
stata nulla (una retta coincidente con l'asse t o delle X), per tutte le
nostre auto. |
 |
Ma se l'accelerazione non è nulla, cioè se la velocità varia?
Studiamo il caso più semplice: se abbiamo studiato il caso del moto a
velocità costante, ora studiamo cosa succede se l'accelerazione è
costante, invece di un moto rettilineo uniforme avremo un moto
UNIFORMEMENTE ACCELERATO. |
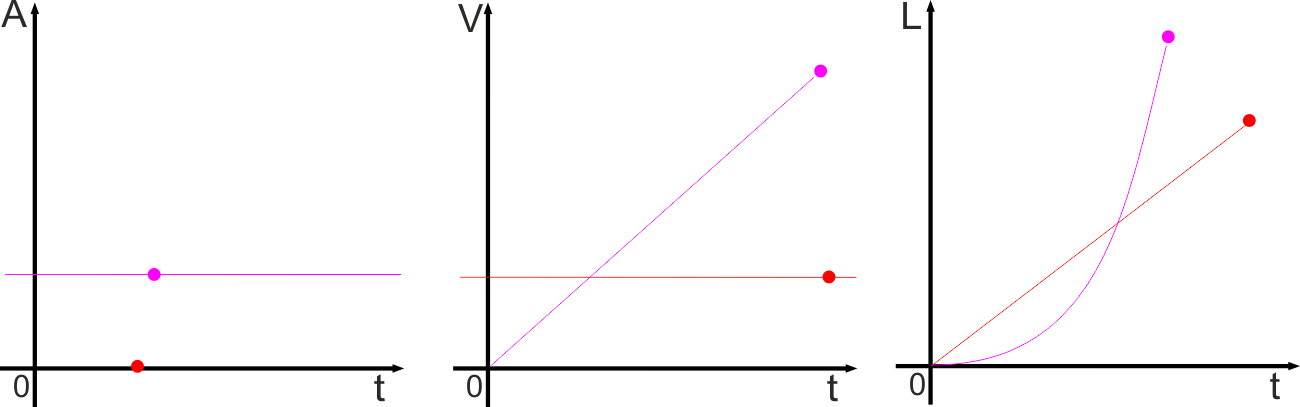 |
Vediamo sui grafici ...
La pallina rossa si muove con accelerazione nulla, è il caso che abbiamo
visto prima: la velocità può essere solo costante, e quindi il moto
risultante avrà la forma di una retta (pallina rossa).
Se invece la pallina viola si muove con accelerazione costante sarà la
sua velocità a variare in modo uniforme nel tempo ... e lo spazio?
La nostra pallina si muoverà a velocità sempre più grande, cioè man mano
che andiamo avanti nel tempo la linea che rappresenta il suo movimento
nel tempo si comporterà come le rette che abbiamo visto prima: più le
auto erano veloci e più le rette erano "ripide" quindi la linea, se la
velocità aumenta, continuerà a diventare più ripida man mano che passa
il tempo (pallina viola). |
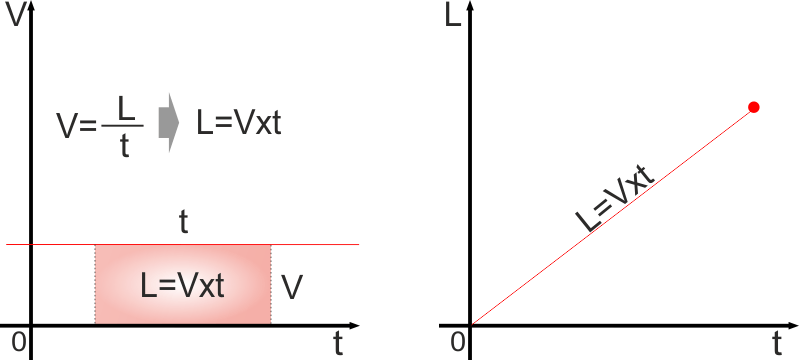 |
Proviamo "quantificare" la cosa.
Facciamo un passo indietro, torniamo alla nostra velocità costante. In
quel caso la velocità era il rapporto tra spazio e tempo (V=L/t) e di
conseguenza, avendo la velocità e volendo calcolare quanto spazio
percorriamo dovremo moltiplicare la velocità per il tempo trascorso (se
faccio 120 km/h per un'ora e mezza farò 120x1.5 = 180 km).
E volendo raffigurare la cosa nel nostro grafico, L=Vxt è come dire
l'area del rettangolo che ha per base il tempo trascorso t e per altezza
la velocità V.Nello stesso modo (è un po' meno facile da seguire, ma
è esattamente lo stesso principio) se l'accelerazione è costante, la
velocità possiamo esprimerla come V= Axt e anche in questo caso noj è
altro che l'area del rettangolo che ha per altezza A (che è costante e
quindi resta sempre la stessa) e per base t (che man mano che passa il
tempo aumenta).
|
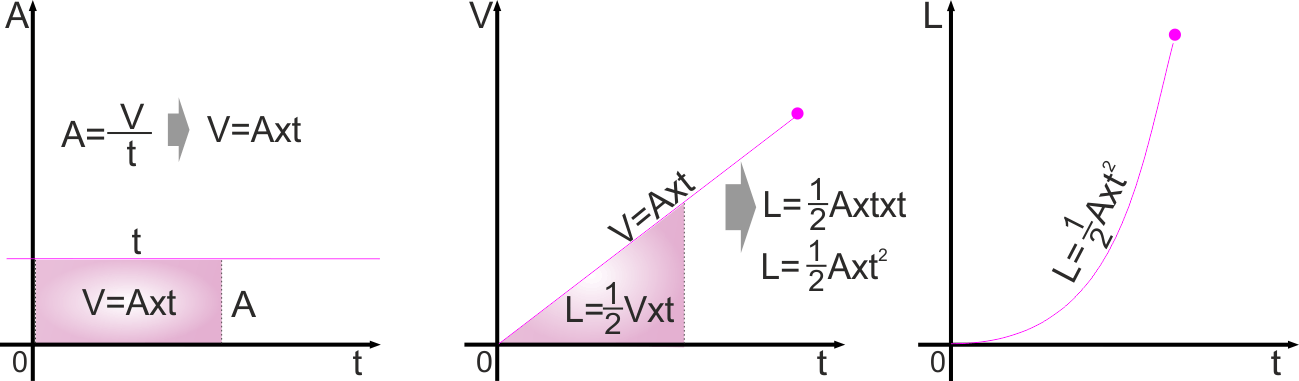 |
E quando poi passiamo dalla velocità allo spazio ...
Uguale a prima, è ancora l'area delimitata dalla linea che rappresenta
la velocità e l'asse X (o del tempo t), solo che questa volta la linea è
inclinata.
Evvabbé, vorrà dire che invece di L= Vxt (area del rettangolo) avremo
L=1/2Vxt (area del triangolo) ...
E siccome V era uguale ad Axt, sostituendo Axt a V abbiamo
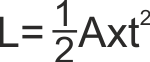
Cioè abbiamo visto che se il moto è uniformemente accelerato lo
spazio aumenta col quadrato del tempo ... nel corso di matematica
abbiamo visto che una curva di questo tipo è una PARABOLA. |
Questo risultato è piuttosto importante, perchè
qui vale la pena di tirare in ballo il SECONDO PRINCIPIO DELLA
DINAMICA , dovuto a ISAAC NEWTON che dice che una forza F
applicata ad un corpo di massa m lo accelera con
un'accelerazione a tale che F=ma
.
Che per essere il più semplici possibili vuol dire che se
applico ad un corpo una forza costante, quello si muoverà di
moto uniformemente accelerato.
Il caso più comune è quello di un oggetto lasciato cadere ... se
trascuriamo le forza viscose (l'aria .. supponiamo di far cadere
il nostro oggetto nel vuoto) questo si muove di moto
uniformemente accelerato ... Galileo Galilei dimostrò che questa
accelerazione era costante e non dipendeva da come era fatto il
corpo o dal materiale con cui era costruito.
Gli astronauti della missione Apollo 15 lo provarono fuori da
ogni possibile dubbio: Davd Scott lasciò cadere a terra (a Luna,
veramente) contemporaneamente un martello e una piuma, e questi,
non essendoci aria sulla Luna, toccarono il suolo nello stesso
istante. |
 |
|
Per completare la trattazione precisiamo ancora un paio di cosette:
questa "formula" che da il moto di un corpo soggetto ad una
accelerazione costante, manca ancora di qualcosa ...
Cioè abbiamo studiato come l'accelerazione influisce sul moto, ma
abbiamo immaginato un oggetto che partisse da fermo.
E se invece avesse gia avuto una sua velocità?
Niente di impossibile, la sua velocità si mantiene costante e si somma a
quella dovuta all'accelerazione.
E questo non solo in forma "semplice" (vengo "sparato" a 100 km/h verso
l'alto, ad esempio, e sono sottoposto all'accelerazione di gravità ..
per cui rallento .. la mia velocità sarà V0
- axt ,
e lo spazio percorso sarà V0xt
- 1/2 axt2
+ L0 , dove L0
sarà la quota alla quale sono partito), ma anche in forma "vettoriale",
cioè scomponendo il moto nelle sue componenti verticale ed orizzontale
...
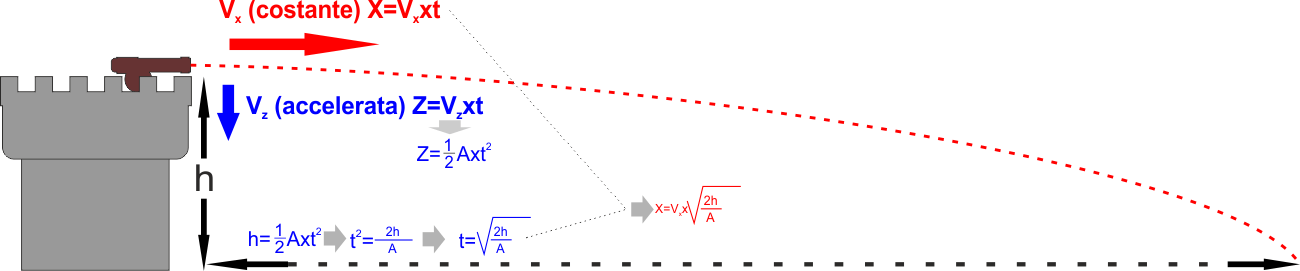
Supponiamo di essere sugli spalti di un castello e di sparare un colpo
di cannone in direzione orizzontale ad una velocità Vx .. il
proiettile si muoverà in orizzontale a velocità costante, mentre verrà
accelerato verso il suolo con accelerazione costante ... se vogliamo
sapere dove andrà a cadere basta vedere quanto tempo impiega a toccare
terra, che per capirci è lo stesso tempo che impiegherebbe se fosse
semplicemente lasciato cadere dalla stessa altezza senza essere
"sparato", |
 |
| Vi anticipo, ma lo vedremo meglio nel prossimo
capitolo, che l'accelerazione di cui stiamo parlando, l'accelerazione di
gravità, la possiamo considerare costante (vedremo poi con precisione
quanto possiamo considerarla costante e perché) e la indicheremo con
g (circa 9.8 m/s2). |
|