|
Se camminiamo nella neve sprofondiamo.
Se camminiamo nella neve con le ciaspole o con gli sci non
sprofondiamo.
Eppure la forza peso che ci "schiaccia" sulla neve è la
stessa, il nostro peso.
Cambia la "pressione".
Nel primo caso la pressione tra la neve e le nostre scarpe è
il nostro peso distribuito sulla piccola superficie delle
suole.
Nel secondo caso lo stesso peso è distribuito sulla
superficie molto maggiore delle ciaspole o degli sci.
|
|
 |
 |
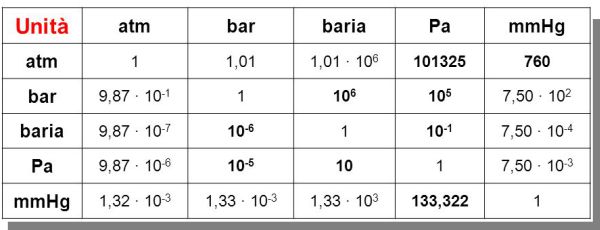
Viene definita PRESSIONE la grandezza fisica che è il
rapporto tra il modulo di una forza ortogonale ad una
superficie e la superficie stessa.
La PRESSIONE si misura quindi in Newton/m2
(Pascal).
Il Pascal (Pa) in realtà è una unità molto
piccola per le nostre usuali necessità (ad esempio la
pressione atmosferica varrebbe circa 101.325 Pascal).
Per cui è normale utilizzare come unità di misura della
pressione multipli del Pascal quali l'ettopascal (hPa)
- in meteorologia sostituisce il "millibar" nella
misura delle variazioni della pressione atmosferica - o il
bar , utilizzato quando abbiamo a che fare con
pressioni elevate (1 bar = 100.000 Pa).
In forma "pratica" la pressione si misura anche in relazione
alla pressione atmosferica. |
Ad esempio quando dal gommista gonfiamo le gomme dell'auto il
valore che leggiamo sul "manometro" (che è lo strumento che misura
la pressione elevate, mentre il "barometro" misura la pressione
dell'aria atmosferica) è in "atmosfere" (una atmosfera è 101.325 Pa
o 1,013 bar, però misura la pressione "relativa", cioè rispetto ad
uno "zero" che è al valore atmosferico, per cui si può scendere
anche a numeri negativi).
Ovviamente non esistono valori negativi della pressione assoluta
(atmosfera zero corrisponde al valore del vuoto, e ovviamente non si
può togliere gas da un posto dove non ce n'è).
Come sempre gli anglosassoni hanno le loro unità di misura "fuori
dal coro" - il più frequente è il psi (Pound per Square Inch -
Libbra per pollice quadrato) - in genere sui manometri sono
riportate diverse scale di misura.
 |
E' importante fare bene attenzione a quale scala stiamo
utilizzando - nella figura a fianco vedete una gomma
automobilistica gonfiata ad una pressione di 1,8 bar
(differenziale, vuol dire che la pressione è di 1,8 bar
rispetto alla pressione esterna, e quindi di 2,8 bar in
assoluto). Sul manometro è riportata anche la scala in psi e
notate che "credere" di aver gonfiato a 2 bar perché la
lancetta è sul "20" vorrebbe dire aver gonfiato a solo 1,5
bar nello stesso modo se dovessimo gonfiare qualcosa a 40
psi e ci fermassimo a 4 bar correremmo il rischio di vederci
"scoppiare" lo pneumatico.
In medicina si utilizzano i mmHg (millimetri di mercurio o
Torricelli torr) per misurare la pressione del sangue,
misura basata sul funzionamento dei vecchi manometri a
mercurio. |
 |
 |
|
|
LA LEGGE DI
PASCAL |
Quando gonfiamo un palloncino, un gommone, uno pneumatico, questo
assume ovunque la stessa "consistenza".
Ovunque "premiamo" sul nostro oggetto gonfio, la resistenza che
incontriamo è sempre la stessa.
Possiamo quindi dire che dalla nostra esperienza parrebbe che la
pressione esercitata su qualsiasi superficie a contatto con il
fluido (qui è aria) sia la stessa ovunque.
Questa è la legge di Pascal, che afferma che la pressione esercitata
da un fluido sulla superficie del suo contenitore (o su qualsiasi
superficie a contatto con il fluido) sia la stessa ovunque (a meno
del peso del fluido stesso come vedremo nel paragrafo successivo
dove parliamo della pressione idrostatica). |
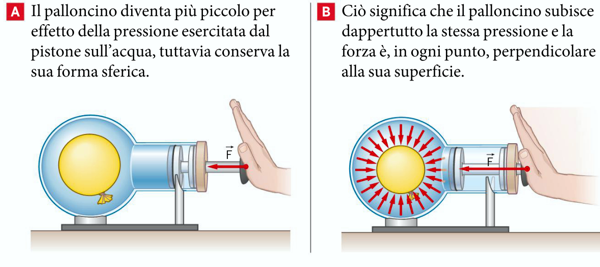 |
Un'esperienza "classica" è quella di inserire un palloncino gonfio
all'interno di un recipiente sigillabile pieno d'acqua e poi con un
metodo qualsiasi, ad esempio una siringa che permetta di "spingerci"
dentro altra acqua, ne aumentiamo la pressione.
Si osserva che il palloncino all'interno si rimpicciolisce (e
successivamente si ridistende se diminuiamo di nuovo la pressione)
in modo simmetrico.
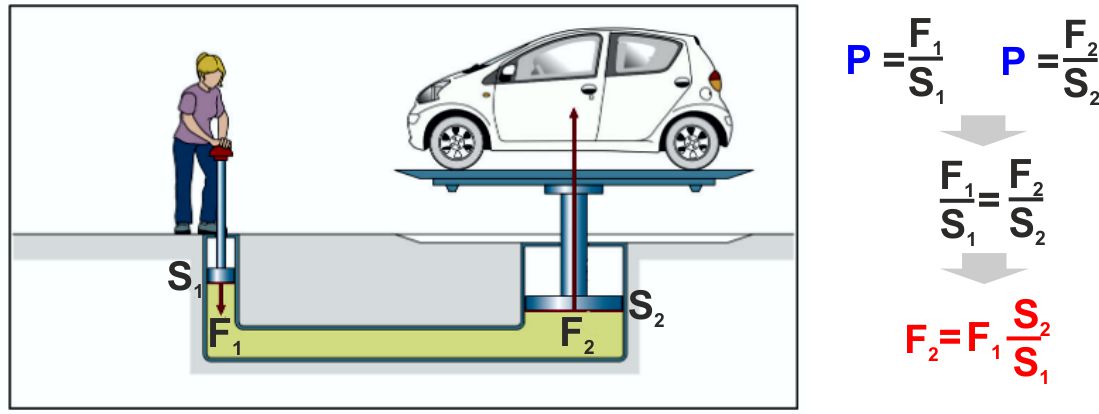
Un'applicazione di questo principio è ad esempio il TORCHIO
IDRAULICO.
Il principio è quello per cui se io aumento la pressione in un
contenitore spingendo un liquido mediante un pistone con una forza F1
una superficie piccola S1, otterremo una pressione F1/S1
all'interno del contenitore.
Se a questo colleghiamo un cilindro con un pistone con una
superficie molto più grande S2 (supponiamo ad esempio che
S2 sia 100 volte S1).
La pressione F1/S1 si distribuirà sulla
superficie S2 che spingerà il pistone con una forza F2
= F1/S1 x S2 - se il rapporto tra S2
e S1 è 100 a 1, la forza F2 sarà 100 volte la
forza F1. |
 |
|
LA LEGGE DI
STEVINO |
|
 |
Se facciamo una colonna umana
come nella figura a lato la ragazza in alto non sentirà
nessun peso sulle spalle, il ragazzo sotto di lei avrà sulle
spalle il peso della ragazza, quello ancora sotto dovrà
sopportare il peso del ragazzo più quello della ragazza, e
sulla scala sotto i piedi del terzo il peso sarà la somma
dei pesi della ragazza e dei due ragazzi.
Nello stesso modo Se ho un recipiente pieno d'acqua l'acqua
in alto si "appoggia" sullo strato d'acqua sottostante,
questo su quello ancora sotto, e questo su quella ancora
sotto ...
Man mano che scendo aumenta il peso che l'acqua deve
sopportare.
Se considero una superficie di riferimento qualsiasi questo
"peso" diventa pressione. |
 |
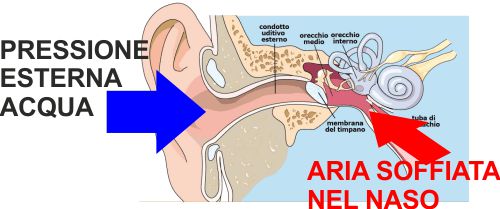
Lo sappiamo bene, almeno noi genovesi che in
mare ci siamo praticamente nati: quando scendiamo sott'acqua
la pressione aumenta e ci da fastidio alle orecchie (e
dobbiamo "compensare soffiando aria nel naso dopo essercelo
tappato in modo che non possa uscire e vada a "compensare"
la pressione esterna spingendo sul timpano).
Ogni liquido ha una sua "densità", cioè massa per unità di
volume (kg/m3).
Per l'acqua è (ovviamente direi, visto che abbiamo definito
un kg di massa proprio la quantità d'acqua che occupa un dm3
di volume) 1.000x9.8 N/m3. |
 |
Ogni volta che scendiamo di un metro,
quindi, se consideriamo una superficie di un m2,
il peso aumenta di 1.000 kgp (peso, in Newton sono sempre
1.000x9.8=9.800 N) ...
La pressione di conseguenza aumenta di 9.800 N/m2
(9.800 Pa)
Ogni 10 m saranno 98.000 Pa (se ricordiamo che la pressione
atmosferica è di 101.300 Pa vuol dire che la pressione
aumenta circa di una atmosfera ogni 10 m).
Un'esperienza classica consiste nel prendere un recipiente
con un ragionevole sviluppo verticale (parliamo di una
bottiglia di plastica) e praticare tanti forellini ad
altezze diverse.
Se la riempiamo d'acqua vedremo che questa esce dai
forellini spinta da pressioni diverse.
Il getto vicino alla base della bottiglia sarà più potente
di quello che vedremo uscire dai fori più in alto.
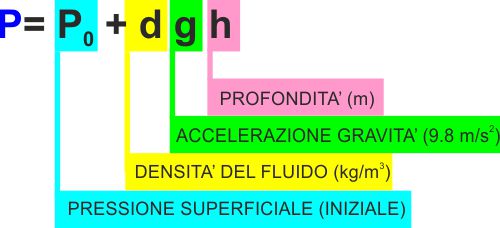
La legge di Stevino in pratica dice che la pressione
aumenta con la profondità con la legge P = P0
+ dgh, dove P0 è la pressione che c'è
sulla superficie del liquido (se parliamo di acqua di mare è
la pressione atmosferica al livello del mare), d la
densità del liquido, g la solita costante che ci da
l'accelerazione di gravità sulla Terra, e h la
profondità. |
 |
|
 |
La pressione dovuta alla profondità (la parte dgh) è
detta PRESSIONE IDROSTATICA.
Secondo la legge di Stevino quindi la pressione è funzione
solo della densità del fluido e della profondità.
E infatti, comunque sia fato il recipiente che utilizziamo,
alla stessa profondità avremo sempre la stessa pressione (ad
esempio anche un tubo sottile che porta acqua da un palazzo
alto 50 metri, nella parte più bassa dovrà sopportare una
pressione di 1+5= 6 atmosfere).
|
|
|
IL PRINCIPIO DI
ARCHIMEDE |
Come abbiamo visto la pressione aumenta con la
profondità.
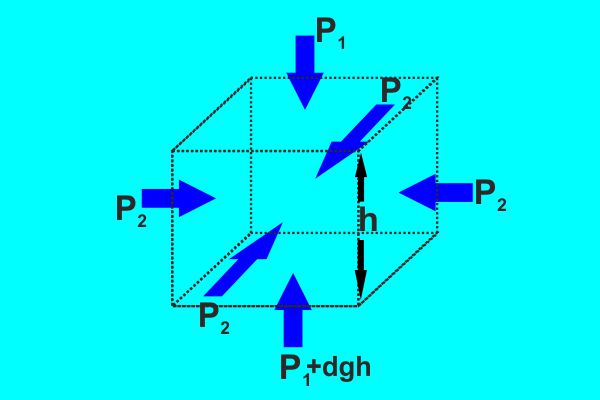
Se consideriamo un "cubo d'acqua" all'interno di una vasca e
andiamo a valutare le pressioni sulle superfici (ideali) di
questo cubo, vedremo che :
- Le pressioni P2 che agiscono sulle facce
frontali e laterali del cubo devono essere per forza
tutte uguali (se no l'acqua si sposterebbe a destra o a
sinistra, mentre invece è ovvio che stia ferma)
- La pressione che agisce sulla faccia inferiore deve
essere per la legge di Stevino uguale a quella che
agisce sulla faccia superiore P1 più
l'aumento di pressione idrostatica dovuto alla
differenza di profondità h tra la faccia superiore e
quella inferiore.
E' immediato vedere che dgh, moltiplicato per la
superficie della base del cubo, da il perso del liquido
contenuto nel cubo.
E' anche immediatamente intuitivo comprendere che se il cubo
sta fermo (non sale e non scende) vuol dire che in qualche
modo riceve una spinta (appunto dalle pressioni
differenziali tra la faccia inferiore e quella superiore)
che compensa il suo peso.
Ovvero che, come recita il principio di Archimede.
UN CORPO IMMERSO IN UN LIQUIDO RICEVE UNA SPINTA DAL
BASSO VERSO L'ALTO PARI AL PESO DEL LIQUIDO SPOSTATO.
Che vuol dire che (ovviamente), se io tolgo il liquido e
al suo posto metto un cubo reale, solido, che però ha le
stesse dimensioni e lo stesso peso del cubo d'acqua che ho
tolto, anche questo starà fermo (non sale e non scende). |
 |
|
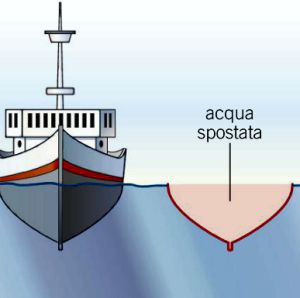 |
Quindi in pratica se io costruisco un oggetto che
immerso in acqua ne sposta (disloca, questo tipo di scafo si
chiama appunto "dislocante") una quantità tale da eguagliare
il suo peso, l'oggetto galleggia.
Se io riempio questo spazio con materiale pesante, quando
supero il peso dell'acqua che lo stesso volume avrebbe
potuto contenere, il mio oggetto affonda.
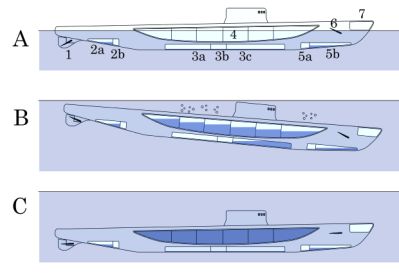
E' così che funzionano i sommergibili.
All'interno del sommergibile vi sono delle casse d'aria che
fanno si che l'acqua "spostata" dallo scafo del sommergibile
sia di più del peso del sommergibile stesso.
Quando voglio far scendere il sommergibile io pompo acqua
dentro lo scafo in modo da appesantirlo, fino a che il suo
peso sia uguale quello dell'acqua che occuperebbe lo stesso
volume del suo scafo,a questo punto il sommergibile avrebbe
un assetto "neutro" (cioè messo ad una certa profondità non
tenderebbe né a salire né a scendere.
Per scendere si utilizzano quindi i timoni di profondità
(superfici idrodinamiche che funzionano come il timone di
profondità degli aerei) e la spinta del motore.
Per farlo risalire basterà lasciare uscire quest'acqua
(spinta dall'aria in pressione delle casse) e il
sommergibile risalirà. |
 |
|
 |
Il corpo umano sotto il profilo del galleggiamento è
"positivo", cioè un corpo umano "nudo" (senza pesi
aggiuntivi) immerso in acqua riceve una spinta tale da farlo
galleggiare.
La condizione però è che il corpo sia IMMERSO nell'acqua.
Se infatti io mi "sdraio" sull'acqua immergendo la testa (la
nuca), in effetti galleggio senza fare nessuna fatica.
Ma allora perché la gente affoga???
Perché se io cerco di tenere la testa fuori dall'acqua il
volume immerso diminuisce e quindi diminuisce anche la
spinta, e il mio corpo scende.
Non "affonda", ma scende quel tanto da farmi andare la bocca
sott'acqua, se a questo punto io mi agito cercando di alzare
(quindi togliere dall'acqua, quindi diminuire ancora il
volume immerso) le braccia, anche il resto della testa
(e in particolare naso e bocca) vanno sott'acqua.
Come nei sommergibili anche noi abbiamo delle "casse
d'aria", i nostri polmoni.
Quando sono pieni d'aria la spinta idrostatica aumenta,
quando li svuotiamo diminuisce.
Basta respirare con calma evitando di svuotare i polmoni e
il nostro corpo galleggerà senza fatica. |
 |
|
|